PDF File: (Click to Down Load): Chapter4.pdf
Related Web Page on EM radiation and Spectrum
Chapter 4. Electromagnetic Radiation in Analysis (Chapter 3 Campbell & White).
Electromagnetic radiation is a disturbance in electro-magnetic space which follows Maxwell's differential equations for conversion of energy from an electrical field to a magnetic field. The disturbance is sinusoidal in nature for propagating EM radiation.
Electromagnetic waves display a wave nature in that the oscillating electric and magnetic fields propagate with a wavelength and frequency. Additionally, a special property of EM radiation is that it displays a fixed speed in vacuum, c, and fixed velocities in other uniform media so conversion from frequency to wavelength is direct:
n
=c/lWe can specify a type of EM radiation by specifying it's wavelength, frequency, or wavenumber, k:
k = 1/
lEM radiation also displays a particle characteristic through the concept of the photon which is a particle of no mass. This allows a means to describe features of EM radiation which are usually associated with particles such as momentum.
The energy per photon of EM radiation is related to the frequency,
n, of the Maxwellian sinusoidal oscillation through Planck's constant, h:Energy = h
nThat is, higher frequency is associated with higher energy. Then the Energy is given by hc/
l and different wavelength radiations contain different amounts of energy per photon. A photon is a quantum of EM radiation that displays momentum. The momentum is expressed as:p = h/
l =hn/cThe brilliance, brightness, flux or intensity of a particular EM radiation is related to how many photons are delivered in a unit area per unit time. The energy of each photon is related directly to the wavelength. It is important to be able to distinguish in your mind between intensity, energy and power delivered by EM radiation.
The energy of EM radiation determines the effect of the radiation on materials and is the basis for understanding analytic techniques which use EM radiation. The intensity determines the amount or number of these effects which occur. For example, x-rays are of short wavelength and have very high energy per photon. Because of this x-rays are a type of ionizing radiation which can cause cancer in humans through formation of free radicals in your DNA for instance. Radio waves are of very large wavelength and low energy. Radio waves pass through our bodies constantly with no effect. High intensity radio waves can cause changes in the spin polarization of nuclei when the nuclei are under a very strong magnetic field and this is the basis of nuclear magnetic resonance absorption which will be discussed in class.
Features of Electromagnetic Waves:
1) EM waves are described using a sin function in time and space. That is, at a fixed time the wave varies in Amplitude, A, with spatial position and for a given position in space the wave varies in amplitude with time. This is true of both the electric field vector, E, and the magnetic field vector, B.
E = A sin[2
px/l -2pnt]B = B0 cos[2
px/l -2pnt] Out of phase with E by 90°E and A have direction.
l is the wavelength, n is the frequency.2) The frequency and wavelength are related by the velocity of the EM wave which in vacuum is c, "the speed of light".
l = |c|/n
c = 3 x 108 m/s
3) The amplitude is related to the "intensity" of the EM radiation:
Intensity = |A|2
Intensity doesn't have direction, amplitude does.
4) The energy of EM radiation is directly related to the energy associated with phenomena by which it is made and is not associated with the intensity. Planck's law states:
Energy/photon = h
n = hc/lh = 6.63x10-34 J s
The idea that EM radiation has an energy is tied to the particle view of EM radiation, i.e. there is a particle called a photon which has no mass which carries the EM energy and has momentum, p.
p = h
n/c = h/l (c/c)5) Light, X-rays and other EM radiations are generally composed of a number of photons so one can consider the relationship between different waves in a beam.
i.) Coherent: If all waves in a beam are in-phase, that is have the same phase angle (peaks of waves coincide in space) they are called coherent. Waves which are not coherent can interfere with each other leading to a reduction of the intensity. For example, a laser beam is coherent while a flash light beam is incoherent. This is one reason why a laser beam can propagate over great distances while a flash light beam quickly dissipates.
When considering interference of two waves one adds or subtracts amplitudes of the electric field vector E. The intensity which is measured is the square of the resulting amplitude, #3 above.
ii.) Collimated: Beams with waves which are all progressing in the same direction are termed a well collimated beam. Collimation refers to the divergence of the waves in a beam. A light bulb produces uncollimated light which spreads in all directions. The sun's rays, when they reach earth are well collimated since the angular divergence is low. A laser beam or a synchrotron x-ray beam are well collimated due to the mechanism by which the EM radiation is produced.
iii.) Monochromatic: If all waves have the same frequency (or wavelength by #2 above) they are called monochromatic (one color). A source like a light bulb, the sun, or an x-ray tube generates polychromatic (white light) radiation (many wavelengths) and a source like a laser or an x-ray synchrotron yields monochromatic radiation.
The polychromacity of EM radiation is tied to the mechanism of formation. If the formation event is specific (quantum) in terms of the energy transfer associated with the formation event, monochromatic radiation results. If the formation event is statistical (distributed in energy) polychromatic radiation results.
iv.) Polarization: The electric field vector, E, for and EM wave has a direction in a plane normal to the propagation direction. If the direction is fixed relative to the propagation direction and this direction is the same for all waves in a beam, the EM radiation is said to be linearly polarized. Polarization can be produced by a number of means: Reflection off a surface leads to linear polarization in the plane of the surface, highly birefringent materials can lead to polarization of a beam by absorption of components not with a certain polarization, some processes for formation of EM radiation produce polarized radiation laser and x-ray synchrotrons, in some cases a grating can be used to polarize radiation (Soller slits for x-rays), diffraction leads to polarized radiation depending on the geometry of diffraction.
In addition to linear polarization, waves can be elliptically and circularly polarized. In circularly polarized beams the vector E rotates in direction along the propagation direction. Elliptically polarized radiation is a mixture of circularly and linearly polarized radiations, i.e. there is some rotation of the vector E but it is not symmetric. In this class we will only discuss unpolarized and linearly polarized radiation.
7) EM radiation can always be assumed to travel in a straight line.
8) EM radiation interacts with matter in different ways depending on the energy associated with a photon. That is, energy decides what happens while intensity decides how much happens. Radio waves are low energy/high wavelength (see table above) and can pass through most materials with no effect. IR vibrates bonds and can generate heat. Light changes the polarization of molecules which is a minor effect. UV can dissociate weak bonds and cause degradation. X-rays are a type of ionizing radiation that can ionize atoms and molecules. Typically, x-rays have wavelengths on the Ångstrom scale. Generally, the lower the wavelength of radiation the higher the danger due to the higher energy associated with short wavelengths see #4 above. It is also more difficult to produce and use high-energy photons since they must result from an associated high energy event and they are absorbed by most materials through the interactions mentioned above.
9) For visible light the index of refraction, n, is used to describe the speed of the radiation in a medium.
Velocity = v = c/n.
Since the velocity is always smaller than the velocity in vacuum, n is always greater than 1. In air, n is close to 1, in silica glass n = 1.52, some materials have a very high index of refraction, Titania, TiO2, is close to 5.
Beer-Lambert Law:
As a first approximation all EM radiation can be considered to follow a linear absorption behavior described by an exponential decay of intensity with thickness of a sample and with concentration of the absorbing species. This is critical to quantitative analysis using EM absorption which is the basis for IR, NMR, and UV spectroscopies. The Beer Lambert Law states that the value of the absorption is proportional to the amount of the absorbing species.
In a typical absorption experiment, a beam of EM radiation passes through a sample of thickness "t". For a small thickness, dx, the incident intensity at wavelength
l and position x, I(x), is reduced by dI due to absorption by the sample. The change in intensity is proportional to the thickness, dx, the incident intensity I(x) and the linear absorption coefficient, A:![]()
For a thicker sample this equation can be rearranged and integrated:
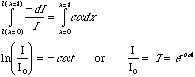
"T" is the transmission ratio for the sample at wavelength l, and A = c
a is the Absorption. The Beer-Lambert Law given above gives t A = ln(1/T). Absorption spectra are either plotted as transmission or as absorption on the y-axis. In a transmission plot the absorption peaks point down. In an absorption plot the absorption peaks point up and are the ln of 1/T as above.Scattered Intensity:
For a scattering experiment such as XRD, SAXS, or Raman scattering the Intensity is plotted versus either and energy or angular term. The integrated intensity for a scattering peak is directly proportional to the amount of the scattering material. A Raman scattering experiment results in data which looks very similar to an IR absorption experiment with both plotted versus wavenumber = k = 2
p/l. IR will be a plot of Transmittance (peaks down) or Absorption (peaks up) and a Raman pattern will be a plot of Intensity (peaks up).Instrumentation for Spectroscopy:
Dispersive Spectrometer:
Figure 4.1 of Campbell and White, pp. 44, shows a typical dispersive optics spectrometer (UV in this case). Even in this simple instrument the optical paths are quite complicated. The first requirement of a spectrometer is resolution of the spectrum of an source through a tunable device which can isolate a single wavelength radiation. In a dispersive instrument this can be done with a prism or with an optical grating. The prism disperses the incident radiation due to differences in the index of refraction of the glass prism with wavelength, n(
l). Snell's Law can be used to determine the angle of refraction of different wavelengths:nAir sin(
qAir) = nGlass sin(qGlass)where qAir is the angle of the incident beam with respect to a normal to the surface of the glass, and qGlass is the angle of the beam in the prism with respect to the glass surface normal. The double refraction of the prism serves to disperse the incident beam into angularly diverging beams of different wavelength. The prism can be rotated to select certain wavelengths using a slit. An optical grating can also be used to disperse wavelengths using Bragg's Law:
sin(q)=l/2d
where 2q is the angle of divergence from the incident beam.
The main problem with dispersive instruments is that almost all of the incident radiation is lost in the slit arrangement for selecting a diverging beam of the desired wavelength. The measurement of a spectrum involves rotation of the prism or grating.
Most spectrometers involve double beam optics (shown in Figure 4.1) because,
1) the source has a spectrum of its own,
2) imperfections in the prism or grating might selectively effect certain wavelengths,
3) the detector usually has a spectral sensitivity which varies with wavelength and
4) the instrumental sensitivity might vary in time due to atmospheric interference and fluctuations in the electronics.
Double beam optics are achieved by a partially silvered mirror which effectively splits the incident beam into two beams, a Reference beam and the Sample beam. A reference cell is used which duplicates the sample except that no sample is present. A rotating mirror is used to alternatively sample the reference and sample beams and the transmission is measured as the ratio of these two beams using a photomultiplier (PM) tube which results in a number of counts or events. The raw counting error for such a spectrometer is related to the square root of the number of counts measured by the PM tube. Usually, this counting error is much smaller than the error introduced by the instrumental setup such as the spectral width attainable with the slit/prism optics.
Fourier Transform Instruments:
The loss of information due to the dispersion/slit optics in a dispersive spectrometer was long known to be a major hindrance to the determination of EM absorption spectra. With the development of the Michelson Interferometer a route to alleviate this problem became clear. Figure 5.2 of Campbell and White, pp. 57, shows a schematic of a Fourier Transform IR absorption spectrometer. The Fourier transform instrument results in an interference pattern between two EM beams which is the Fourier equivalent of an absorption spectrum. Fourier transform mathematics are critical to IR and Raman spectrometers, NMR spectroscopy, and is the basis for scattering techniques such as XRD, SAXS and SALS we will spend some time discussing FTIR instruments as a simple introduction to Fourier techniques in Polymer Analysis.
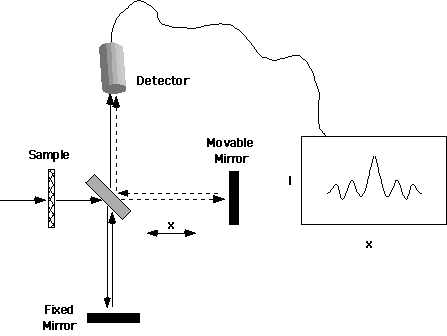
Consider the instrument shown schematically above. Polychromatic radiation (see definition above) is incident on a sample and the intensity versus wavelength spectrum is modified by absorption of radiation at certain characteristic wavelengths by the sample (see below). A polychromatic spectrum is composed of a series of EM waves of different wavelengths, with different amplitudes. This continuous distribution of wavelengths can be decomposed into the plot shown below, i.e. Intensity = |A2| versus wavelength. That is, the intensity versus wavelength plot is a population distribution plot for these sine waves. A basic premise of Fourier Theory is that the components of this distribution can be treated independent of the other components. This approach allows us to consider a single sine wave from the polydisperse distribution, and recombine the separate sine waves into the polychromatic spectrum after considering interference and absorption for each wavelength independently.
Consider a single monochromatic sine wave which enters the double mirror at the center of the FTIR schematic above. Identical sine waves propagate to the movable mirror and to the fixed mirror. If the distance traveled to the fixed mirror is L then the path length of the Fixed Mirror beam is 2L. The movable mirror is positioned at location L+x from the central double mirror. The path length for the movable mirror on return to the double mirror is 2L + 2x, and the path length difference for the two beams at the double mirror is 2x. The two beams, one from the Fixed Mirror and the other from the Movable Mirror, are recombined as they progress directly upward in the schematic. The combination of these two beams allows for interference to occur between the two beams, i.e. the phase difference 2p (2x/l) will lead to some conditions of destructive interference between the two beams (Amplitude of one will be positive and the Amplitude of the other will be negative). Summing the amplitude will lead to a smaller total amplitude for most cases, and this reduction in amplitude will be a cosine wave in 4px/l, with a maximum intensity = |A2| at x = 0.
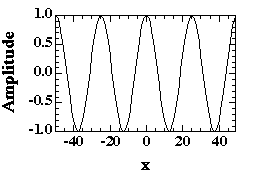
This function is the Fourier transform of a single wavelength, monochromatic, distribution. That is, if we decompose this function into a series of sine waves we find that the function is represented as a single value in the amplitude versus wavelength plot.
Fourier transformation results in inversion of the units of the independent axis. This means that the transformation of x will result in a distribution in wave number, i.e. 1/x =k.
For a monochromatic wave, the interferometer results in a cosine wave centered on x=0. This would result if a laser were incident on the double mirrors, for instance. For a polychromatic wave a series of amplitude versus x plots would result with different wavelengths, across the spectrum of Intensity versus Wavelength shown above. The amplitudes of these polychromatic waves sum after passing through the optics of the interferometer. The resulting sum is a damped cosine wave in x with a central peak at x=0. The decay of this cosine wave is not monotonic, i.e. If the amplitudes at the peaks are plotted against x there is no simple function which describes the decay. The decay contains all of the information concerning the spectra incident on the interferometer. The information, however, can not be directly interpreted from the decay pattern since it is in "inverse space". Inverse space refers to the x-dimension here. This is inverse in units to the wavenumber, k. Real space in this experiment is wavenumber. These two spaces are related by a Fourier transform.
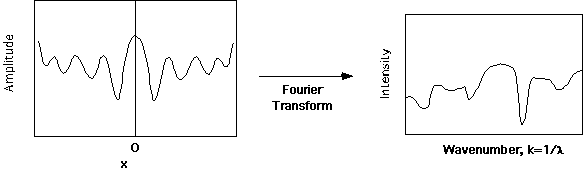
The biggest advantage of a Fourier transform IR instrument over the dispersive instrument discussed above is that all of the incident wavelengths are used in determining the spectrum, i.e. none of the incident radiation is disposed of. In the dispersive instrument almost all of the incident radiation is removed by the slit, see above. The narrowest resolvable feature in wavenumber space is much smaller in a FT instrument. There are a number of other more complicated advantages to the Fourier Transform instrument which will not be discussed here. Dispersive instruments are cheaper since they do not require a computer, a sub-micron translation stage, i.e. x has to be on the scale of the wavelength of light, and a number of other optical components needed in the FTIR instrument. There is also some advantage to a dispersive instrument when the interest is on a single or very narrow range of wavelengths. Pages 57-58 of Campbell and White discuss the FTIR instrument. The governing equation for the Fourier transform in FTIR's is given there as,
![]()
(note error in the equation in Campbell). G is the intensity in frequency or wavenumber space and I is the intensity measured as a function of x. This integral states that the Intensity as a function of n is a sum of cosine waves of frequency n in x space. Fourier transforms are invertable so we can also say that this equation implies that the sum of intensities in frequency space at a position x yield the intensity as a function of x. The basic idea is that intensity can be decomposed into independent sine or cosine components of different amplitudes in either x or frequency space.
Fourier Transforms in Other Analytic Techniques:
Several other analytic techniques rely on either Fourier Transform instruments or Fourier Theory to measure analytic features. The most common are NMR, XRD and SAXS.
In NMR an oscillating decay of radiowave emission in time results from a radiowave pulse in time. This is similar to the decay in tone of a guitar string after being plucked. Fourier transform of this time signal results directly in a frequency space spectrum. This will be discussed in detail when we discuss NMR.
In Scattering techniques such as XRD and SAXS, measurements are made in angular space which can be converted to wavevector or "q" by q=4p/l sin(q) where q is half the scattering angle. The units of q are inverse size and a Fourier transform of the intensity in q-space results in the radial distribution function in real space (size space). We will discuss this when we discuss small angle scattering. This topic is also covered in Cullity in his Appendix on inverse space. (note Cullity uses "s" rather than "q". These two quantities are related by a constant factor of 2p.)