=>Back To Characterization Lab
Download this page: =>MolecularWeight.pdf
Determination of Molecular Weight
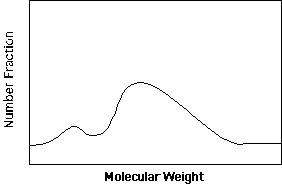
The distinguishing feature of commercial polymers is that they have molecular weights far in excess of the entanglement molecular weight of about 10,000 g/mole. From typical industrial synthesis a fairly broad distribution in molecular weight results. The features of this distribution have dramatic effects on the processability (viscosity) and properties (miscibility, strength and modulus) of plastics. Consider a plot of the fraction of a plastic sample with a specified molecular weight versus molecular weight as show below.

The distribution shown above is bimodal (two identifiable peaks) and skewed (neither of the peaks is a symmetric about their means and the entire bimodal distribution is not symmetric about the mean. Such a distribution of molecular weights can be described by statistics in terms of moments. (see: =>Statistical Descriptions)
The simplest description of a unimodal (one peak) symmetric distribution (same on both sides of the peak) will involve two parameters, the mean, m and the standard deviation, s. More complicated continuous distribution functions will involve higher moments of the distribution. The k'th moment of a distribution about a value, xs, is given by:
![]()
where fi is the fraction of all measurements which have the value xi, i.e. Ni/N, xs is basis for the moment and k is the order of the moment. For example, the mean, m, is the first moment (k = 1) about the origin (xs = 0). The variance, s2, is the second moment (k = 2) about the mean (xs = m).
In polymer science it is the convention to define several special parameters to describe molecular weight distributions. The number average, weight average, z-average and viscosity average. These parameters can be described in terms of the more broadly used statistical description of moments given above.
The number average molecular weight, Mn is the same as the first moment about the origin or the mean. The weight average molecular weight (mass average), Mw, is given by:
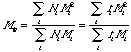
or the ratio of the second to the first moment about the origin.
The polydispersity index, Mw/Mn, is the ratio of the second moment to the square of the first moment about the origin.
Given Mw and Mn the standard deviation of a distribution of molecular weights can be determined:
![]()
The z-average is the third moment about the mean divided by the second moment about the mean.
For a simple unimodal symmetric distribution only the first and second moments are needed to describe the distribution if a functional form such as a Gaussian or Lorentzian distribution is appropriate. For skewed distributions the third moment and perhaps higher order moments are needed such as in the Maxwellian distribution. In general, the number of distinct moments needed to fully describe a distribution is equal to the number of features in the distribution curve. For instance the distribution shown above would require at least two moments to describe the first peak (assuming it is symmetric and could be generated using a Gaussian function), at least three moments to describe the second peak (assuming it can be described by a Maxwellian distribution) and a sixth parameter which relatively weighted the two peaks of the bimodal distribution. Such a bimodal distribution could not be fully describe by just Mw and Mn for instance.
Methods for Characterization of Molecular Weight
Analytic techniques for the determination of molecular weight can be broken down into primary and secondary techniques based on whether or not standards are needed to calibrate the analytic instrument.
Many primary or absolute techniques are based on colligative properties of the polymer such as melting point depression, vapor pressure and osmotic pressure. Other primary techniques use scattering and chemical analysis of end groups. None of the primary techniques are used on a routine basis as they all involve a significant effort and generally yield only one moment of molecular weight. Intrinsic viscosity is theoretically a primary technique, in that for the theta solvation conditions secondary standards are not necessary. In usual practice, at non-theta conditions, intrinsic viscosity relies on knowledge of the Mark-Houwink coefficients for the thermal and solvent conditions of measurement.
An absolute determination of molecular weight for a single sample using light scattering, for example, might take the better part of a week including sample preparation, filtration, running the experiment and preparation of Zimm plots. Use of a solution light scattering instrument usually requires prior experience and can be frustrating in that unknown sources of dust in the sample can often corrupt the data.
The most commonly used techniques are relative techniques since sample preparation and the actual measurement are much simpler and more reproducible. Of secondary techniques, gel permeation chromatography (GPC) (also known as high pressure liquid chromatography, HPLC) is the most versatile and useful technique. GPC results in measurement of the entire molecular weight distribution (see figure above) from which any of the moments of molecular weight or common polydispersity indices can be calculated. For a new polymer a GPC is usually calibrated using monodisperse standards, most commonly polystyrene standards, which are available from most chemical suppliers such as Aldrich, Polymer Labs, and Pressure Chemicals. The molecular weight is then given in terms of the equivalent polystyrene molecular weight and must be so noted. Rarely, it is necessary to develop a new set of standards for an unknown sample, most commonly using light scattering. Training for use of a GPC is rapid and useful results are obtained, usually in the first attempt. Sample preparation and measurement of a molecular weight distribution using GPC requires about 1 day.
In the characterization lab two techniques for determination of molecular weight are introduced, intrinsic viscosity and use of the GPC. Intrinsic viscosity measurement is typical of an absolute technique and the purpose of this lab is to introduce the problems which are common to such techniques. Measurement of the intrinsic viscosity can be a frustrating and messy enterprise.
Intrinsic Viscosity:
The Polymer Handbook (3'rd edition Brandrup and Immergut) lists values for the Mark-Houwink equation as well as a concise description of the intrinsic viscosity (by Kurata and Tsunashima) in section VII. Some of this description is summarized below. Also see: =>Physics of Polymer Coil in Dilute Solution and =>Physics of Polymer Coil in Semi-Dilute Solution.
Consider a polymer in solution at low concentrations <1%. The polymer, typically, takes a self-avoiding walk conformation, R a n3/5, associated with good solvent conditions (n is the molecular weight and R is a measure of the polymer size, here the most probable size). If the temperature is lowered to just above the temperature of phase separation, the coil size is reduced and at some point in this decline in size the theta condition is met where the coil follows Gaussian statistics, R a n1/2. A theoretical description of this behavior is given in Polymer Physics Notes Chapters 1 and 2.
A second way to obtain Gaussian scaling is to increase the concentration of the solution. As concentration is increased the coils will begin to overlap. The overlap concentration, c*, can be calculated if an estimate of the coil size is available. For high-concentrations (>40%) and in the melt the presence of a large number of interpenetrating chains leads to screening of the interactions which lead to solvation of the chains. The chains are subjected to a mean-field which means that the interactions between chains and solvent are smeared. Under these conditions the coil can be shown to display Gaussian statistics.
The intermediate regime between dilute and concentrated conditions are not well understood, but have been partially explained in terms of a special kind of statistical transition in behavior between good solvent and Gaussian behavior. The mathematical tool which allows for a description of this transition is called renormalization. Renormalization is one of the major success stories of polymer physics in the past 20 years.
For the purpose of measurement of intrinsic viscosity all of this is of minor importance. The main consequence is that measurements of molecular weight must involve dilute conditions so as to avoid the overlap concentration and complications which basically can not be resolved. The viscosity of such a dilute solution depends on the viscosity of the solvent, h0, and an effect related to the presence of isolated polymer coils in the solution. There is solvent entrapped in a single, isolated coil, but this solvent does not directly contribute to the viscosity since it is shielded from shear flows in the solution by the polymer coil. This is called the non-draining hypothesis and is a basis of intrinsic viscosity measurements. If the solvent in the coil is entrapped, then the isolated polymer coil is from the perspective of a dynamic experiment (here rheology or fluid flow) a sphere whose size depends on the solvation condition of the coil and short range interactions which effect the persistence length of the chain. Stokes law and the Einstein equation tells us that the enhancement of viscosity due to the presence of these "spheres" can be simply described by the first two terms of a power series expansion, h = h0 (1 + k f), where k is a constant defined by for spheres as 2.5, and f is the volume fraction of spheres. The use of only the first two terms is justified as the equation is only appropriate at low concentrations so f2 <<f. The mass per unit volume, c2, is related to the volume fraction, f, by f = c2Vmolar/M, where M is the molecular weight and Vmola is the partial molar volume of the polymer in solution.
The intrinsic viscosity is obtained in the limit of c2=>0 as [h] = (h - h0)/(c2h0). From the Einstein equation, it is clear that [h] = 2.5 f/ c2 = 2.5 Vmolar/M. M/Vmola is essentially the density of the coil, i.e. the coil mass divided by the coil volume. The units of intrinsic viscosity are inverse concentration. Under theta conditions, R a M1/2 and V a R3 a M3/2, so [h] = K M1/2. The constant K depends on primary molecular features such as the persistence length, so for a Gaussian coil can be calculated from first principles.
The determination of the intrinsic viscosity involves a flow experiment, so that the volume and radius involved are not really the end-to-end distance for the coil or the most probably size. A new measure of size, the hydrodynamic radius, RH, and hydrodynamic volume, VH, are needed. These new parameters are assumed to have the same molecular weight dependence as the end-to-end distance and radius of gyration for the coils. The hydrodynamic parameters are essentially empirical, i.e. these are measured and not really fundamental quantities. There is some literature available on a theoretical basis for hydrodynamic measures of size in the colloid literature, much of it based on the work of Simha at Case Western.
Generally, the intrinsic viscosity is measured under non-theta conditions so an empirical equation is used to describe the intrinsic viscosity/molecular weight relationship, the Mark-Houwink equation, [h] = K Ma, where a and K are constants for a specific polymer/solvent/temperature system. At the theta condition a should go to 1/2. For non-theta conditions a>1/2. For good-solvent scaling a is expected to be 3/5. "a" varies from the values of 1/2 or 3/5 due to short-range interactions and their implied effect on the definition of M. Branched polymers can have a value of a less than 1/2. Values greater than 0.6 are usually associated with chain rigidity and asymmetry of the coil due to features such as helical coiling.
The viscometer used to measure dilute solution viscosity is usually a capillary viscometer. This viscometer uses the Poiseuille equation for laminar pressure flow in a capillary tube. The volumetric flow rate, Q = DV/Dt, under gravity, following Poiseuille's law is given by, Q = rgpR4/(8h). For constant volume, DV, the time for flow is proportional to the viscosity, t = kh. (Poiseuille's law for pressure and gravity driven flow is Q = (rgH + Dp)pR4/(8hH).)
Since time is proportional to viscosity, the intrinsic viscosity can be calculated form a capillary viscometer substituting time for viscosity, the limit of c2=>0 as [h] = (t - t 0)/(c2 t 0).
GPC:
Gel permeation chromatography involves passing a dilute polymer solution through a tubular column packed with polymeric gel (crosslinked) beads. Under high pressure flow some of the polymer chains are forced into the pores of the gel, while others pass by the gel beads. The residence time of a given polymer chain in the packed column depends on the path it takes through the gel. For instance, a low molecular weight oligomer will easily be force into the pores of the gel and will take a circuitous path through the column, traveling a distance equivalent to hundreds of the column length. High molecular weight species can not fit into the pores of the gel, i.e. they are excluded, and can pass more directly to the exit of the column traveling a distance roughly equivalent to the column length. The selectivity of this process for molecular weight is outstanding and the range of molecular weights which can potentially be characterized by this technique is only limited by the ability to produce controlled spaced gels. GPC is by far the most versatile technique for the determination of molecular weight in a polymer sample.
GPC is called different names in different fields. Organic chemists call it size exclusion chromatography (SEC), high-pressure liquid chromatography (HPLC), gel filtration chromatography (GFC) and variants of these such as HPSEC, HPGFC, HPGPC. There may be some minor differences but the instruments are basically all the same thing.
In GPC a sample of polymer in dilute solution is injected into the chromatograph at an instant of time, t0. The chromatographic column and pumps are pumping the same solvent, albeit with no polymer. A detector is used to note the overall concentration of polymer in the eluted solvent (solvent which has passed through the column) as a function of time at constant volumetric flow rate, Q. The time at constant flow rate reflects a volume of fluid which has eluted from the column, i.e. the elution volume. The time it takes the polymer to elute from the column is called the retention time, tR, and the elution volume for this time is called the retention volume, VR. If the right gel is inserted in the column for the molecular weight range of interest, the relation between VR and molecular weight is linear, VR = VR,0 - kM, where M is the molecular weight, k and VR,0 are constants for a particular polymer/solvent/gel system. The two constants are determined by eluting two or more monodisperse standards. If monodisperse standards are not available, a reference polymer such as polystyrene is used and the molecular weight is given in terms of a polystyrene equivalent molecular weight.
The detector in a GPC must be linear with concentration. Typically a refractometer, for measurement of index of refraction is used. Many other detectors can be used in a GPC and much of the recent development in liquid chromatography has focused on the use of different detectors such as spectrometers, viscometers and light scattering detectors.
The output of a GPC is considered to reflect the number of chains at a given retention volume or molecular weight. From a GPC curve all of the molecular weight distributions, noted above, can be determined. The GPC is the only simple technique to determine the modality (bimodal, trimodal etc.) of a polymer sample.