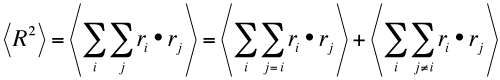
Flory defines a polymer by dynamics as a material controlled by entropy, "Capacity to assume an enormous array of configurations..." P. J. Flory Polymer Chemistry.
Metals/Ceramics/Proteins in the Native State can display essential one configuration, that is the crystal state for metals and ceramics and the native state for a folded protein.
Bond Rotation and Rotational Isomeric States (RISM) for Polymers:
A polymer chain can display many different Rotational Isomeric States. An isomer is a chemically and bonded state that differs from other isomers by bond rotations such as the chair and boat isomeric states of cyclo-hexane. (wikilink)
A polymer chain has many different isomers that can transform from one to the other by bond rotations. We can consider the Newman projection of ethane and butane. We compare the available Eavailable = kT energy to the energy on the plot from the Newman projection to consider the probability p(R) that a conformation will change, where R is the end-to-end distance for the butane chain, for example. For a polymer chain there are many butanes hooked together so things get a bit more sticky but basically we consider energy barriers of the same type compared to the thermal energy, kT, to obtain an expression p(R). This was first (more or less) described in PJ Flory's second book, Flory II or The Statistical Mechanics of Long Chain Molecules (for which he won the Nobel prize). This book is a bit deep for undergraduates but it contains some useful information if you are really interested in the details of a bottom up approach to describing the energy states of polymers.
Polymer chains move randomly due to thermal energy, kT, and if we consider a reference frame centered at one end of the molecule and think of the probability p(R) that the other end is a distance R from the center, the maximum probability will occur at R = 0 since it is equally likely that the chain will be + x and -x for a random chain. It is unlikely that the chain will be fully extended where R = Nl, N being the number of steps of length l in the chain. The function that describes the probability from the R=0 maximum to high values of R is a function that describes a random system, the Gaussian function or the bell shaped curve function used for grade distributions. This function is symmetric about 0 so it must depend on R2 rather than odd powers of R. The curve follows an exponential decay who's breadth depends on the average value of <R2 >,
p(R) ~ exp(3R2 /(2<R2 >))
We can arrive at a value for <R2 > by considering that,
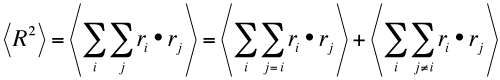
In the first term ri and rj are the same step vector and there are N of these in a chain so the sum yields Nl2 where l is the step length. The second term sums to 0 since there are equal probabilities of ri and rj being of opposite sign. Then the square average end to end distance is Nl2, and the probability for a chain of length R scales with,
p(R) ~ exp(3R2 /(2Nl2))
Thermal energy, kT, is not uniform in space or time, as can be seen in the movie below.
Thermal Fluctuations (From http://www.berkeley.edu/news/media/releases/2002/10/24_laser.html)
You should think about thermal energy as a 3d sea of fluctuation values with the average centered on the nominal temperature. Fluctuations occur in both time and space, that is, if we sit at on spot functions occur in time and if we move at a given time we see similar fluctuations in space. The plot above is in space but we also see changes in time. Fluctuations can be of any size so we can possibly overcome any energy barrier, such as in the Newman energy plot. At low energies the probability of overcoming a barrier is low, at higher temperatures the probability becomes higher. Boltzman realized that such probabilities depend on both the depth of the energy barrier, DE, and the temperature and he wrote,
P(R) = exp(- DE/kT)
Where DE is the free energy associated with a chain in the configurational state where it has a length R. By comparing the Boltzman expression with the Gaussian probability we find an expression for the free energy of a polymer chain which serves as the basis for rubber like elasticity,
DE(R)/kT = 3R2 /(2Nl2)
For a chain that is stretched we consider that this energy governs the force associated with stretching. We have that,
FdR = dDE
From Newton's principles. Taking the derivative of DE with respect to R we have,
F = dDE(R)/dR = 3kT/(Nl2) R
From this we see that the polymer modulus (or spring constant), G ~ 3kT/(Nl2), increases with temperature (contrary to normal materials) and that the modulus decreases with molecular weight, N. This is the behavior we observe for elastomers using the molecular weight between crosslinks as N.
For this reason the molecular weight is of primary importance in understanding the mechanical properties of polymers. A similar result is found for the viscosity as shown previously.
DE depends on the chemical composition of the polymer chain as shown with the happy and sad balls in class. DE equally depends on the time or frequency of deformation since the rotation of bonds requires a fixed amount of time to occur. In metals and ceramics deformation involves stretching of bonds in a crystal and formation of defects in the crystal structure that absorb the energy of deformation. These processes are extremely rapid so a time constant or amount of time for deformation is not considered. For polymers, rotation of bonds requires extensive time so each polymer displays a unique characteristic time associated with deformation. Then we consider that the deformation of polymers is equally governed by chemistry, temperature and time.
A good example of this problem can be seen in the First Space Shuttle disaster (Challenger disaster) where rubber engine seals were considered for chemistry and temperature but not for the high frequency (short time) mechanical deformations that occur on liftoff. This failure to understand the importance of the frequency of deformation was noted by Nobel Laureate Richard Feynman in the Congressional Report.