If n is the number of moles rather than
the number of molecules we have,
P = nRT/V.
n/V is the concentration or density of
the gas, φ, and V/n is the specific volume Vsp so we can
write,
P = RT/Vsp = φ RT.
Non-ideal conditions can be considered
in the context of a power series expansion in φ since we expect
non-ideal conditions on increasing concentration given the assumptions
involved in the ideal gas law. A Taylor series expansion is
achieved by using the derivatives of a function at the zero limit so,
P(φ) = RT(0 + φ + P"(φ => 0)/2! +
P'''(φ => 0)/3! + P''''(φ => 0)/4! + P'''''(φ => 0)/5! + ...
or, in the common terms of the virial
expansion,
P/RT = φ + B φ2 +C φ3
+ ...
where B is called the second virial
coefficient and represents the enthalpy associated with binary
interactions in the gas. This same method is used to discuss
solution theory where enthalpic interactions are important to
understanding miscibilty.
A second approach to describing non-ideal behavior is to simply allow a modification of the pressure (to account for enthalpic interactions) and the volume (to account for finite excluded volume of the gas molecules) through the van der Waals equation of state,
A second approach to describing non-ideal behavior is to simply allow a modification of the pressure (to account for enthalpic interactions) and the volume (to account for finite excluded volume of the gas molecules) through the van der Waals equation of state,
(P + a/Vsp2)(Vsp
- b) = RT
where the modification of pressure
follows the dependence of the second virial term, i.e. it depends on φ2.
A third approach is to simply find a correction factor for non-ideal behavior using the compressiblity, z,
A third approach is to simply find a correction factor for non-ideal behavior using the compressiblity, z,
z = PV/nRT
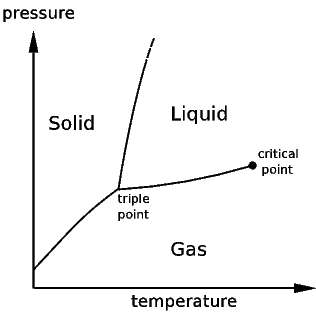
Typically, we use the critical point to
reduce the pressure and temperature to obtain a more universal
compressiblity function. The critical point is the point at which
the density of a liquid and a vapor become the same on increasing
temperature and pressure. Above the critical point liquid and
vapor are not distinguishable and there is no surface tension for
fluids. For CO2 this occurs as 31ºC and 72.8 atm,
for
propane at 97ºC and 42 atm.

The reduced compressiblity is given by,
zr = PrV/nRTr,
where Pr = P/Pc and Tr = T/Tc
and Pc and Tc are the critical pressure
and temperatures.