
=>Back To Characterization Lab
Download this page: =>Semmi-Crystalline Morphology.pdf
2 Crystallinity: Polymer Morphology
Chapter 1 pp. 9, Chapter 2 pp. 13-23, Chapter 4 (all)
General Issues
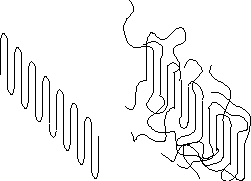
Polymers are unique among engineering materials since they are the only common technological material in which the amorphous state can be the minimum energy state. This is a consequence of topology. Molecular topology is a description of molecules which includes their stereo-chemical arrangement, branching, formation of helices and network/looping/entanglement characteristics. Consider two chains represented using a worm-like model (below)

In the left the chains are not topologically constrained, in the right the chains have a single loop topology and are intertwined. It is impossible for the chains on the right to crystallize even though they may have the same chemical composition and structure as the chains on the left! This is true even at absolute 0 and given infinite time for relaxation (no kinetic effects).
Polymers typically have small diffusion coefficients in the melt and high-molecular weight polymers (above the entanglement molecular weight, about 10kg/mole) have a high degree of entanglement which prevents the chains from reaching an equilibrium structure. Materials such as Polycarbonate are usually used in the glassy state even though they can crystallize under the proper conditions. Usually, better mechanical properties result from lower degrees of crystallinity in polymers. Some polymers such as atactic (common) polystyrene are not capable of crystallizing at all. This is due to stereochemical polydispersity.
Chemical Configuration vs. Conformation.
The terms configuration and conformation are often used interchangeably. It is important to make a distinction between the chemical configuration of a polymer chain which includes block distribution, tacticity groupings and branching as a separated topic from coil conformation which has to do the chain dimensional scaling and size. Local conformation includes helical coiling of the chains (secondary structure in proteins) and formation of larger partially collapsed structures (tertiary structures in proteins). The structure of a chain is intimately tied to the crystalline unit cell and the colloidal shape of crystallites in polymers. The structure of a synthetic polymer chain is polydisperse in all aspects. Structure is built up from,
1) Chemical Configuration- The arrangement of chemical units in the chain. This is known as chain primary structure in proteins.
2) Local Conformation- Rotational states of chemical bonds, formation of helical structures. This is know as chain secondary structure in proteins.
3) Larger scale conformation such as helix folding and formation of "blob" substructures. This is known as tertiary structure in proteins.
4) Global Chain Conformation which is governed by entropy. This dominates the structural scaling of chain size with molecular weight.
Helical structures
Formation of Helical structures is usually required for polymers to crystallize. The formation of long sequences of helical structures requires long sequences of uniform tacticity in chain units. Figures 2.3 and 2.4 (Strobl pp. 18-19).
Trans Gauche conformations in simple vinyl polymers.
Polyethylene is the most common commercial polymer. The secondary structure required for PE to crystallize is a planar zigzag conformation with no helical twist. Polyethylene does not possess tacticity since all substitutent groups are the same. If we consider a Neuman Projection along the chain for two carbons it can be seen that rotation about the C-C bond leads to variable energy states.
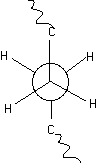
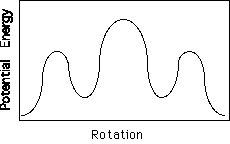
The minimum in this energy diagram (shown to the left) is the trans state. The subminima are the gauche states. The planar zigzag conformation is produced by all trans states.
"Molecular" scale Crystalline Structure:
Consider that we can form an all-trans oligmeric polyethylene sample an bring it below the crystallization temperature. The molecules will be in the minimum energy state and will be in a planar zigzag form. These molecular sheets, when viewed from end will look like a line just as viewing a rigid strip from the end will appear as a line.
Crystal systems are described by lattice parameters (for review see Cullity X-ray Diffraction for instance). A unit cell consists of three size parameters, a,b,c and three angles a, b, g. Cells are categorized into 14 Bravis Lattices which can be categorized by symmetry for instance. All unit cells fall into one of the Bravis Lattices. Typically, simple molecules and atoms form highly symmetric unit cells such as simple cubic (a=b=c, a=b=g=90°) or variants such as Face Center Cubic or Body Centered Cubic. The highest density crystal is formed equivalently by FCC and Hexagonal Closest Packed (HCP) crystal structures. These are the crystal structures chosen by extremely simple systems such as colloidal crystals. Also, Proteins will usually crystallize into one of these closest packed forms. This is because the collapsed protein structure (the whole protein) crystallizes as a unit cell lattice site. In some cases it is possible to manipulate protein molecules to crystallize in lamellar crystals but this is extremely difficult.
As the unit cell lattice site becomes more complicated and/or becomes capable of bonding in different ways in different directions the Bravis lattice becomes more complicated, i.e. less symmetric. This is true for oligomeric organic molecules. For example olefins (such as dodecane (n=12) and squalene (n=112)) crystallize into an orthorhombic unit cells which have a, b and c different while a=b=g=90°. The reason a, b and c are different is the different bonding mechanisms in the different directions. This is reflected in vastly different thermal expansion coefficients in the different directions. The orthorhombic structure of olefinic crystals is shown below. Two chains make up the unit cell lattice site (shown in bold). The direction of the planar zigzag (or helix) in a polymer crystal is always the c-axis by convention.
PE/Olefin crystal structure.
See also, Strobl pp. 155 figure 4.11.
Notes on Crystal Structure From Cullity:(Presented here as a reference)
XRD and Crystalline Structure:
Crystals and the crystalline state can be defined in a number of different ways, density, enthalpy or free energy change on heating, spectroscopic associations, presence of certain planes of registry in microscopy for instance. For XRD a crystal is defined as perfect 3-D order. This corresponds to the strictest definition of a crystal. For a semi-crystalline polymer, for instance, 100% crystallinity is never obtained by this definition since there are large interfacial regions where some degree of disorder is present. Perfect 3-D order means that the structure repeats in all directions so that by describing the structure locally (in a repeating 3-d unit) the entire structure can be uniquely described.
Nomenclature
Point Lattice = An array of points in space so arranges that each point has identical surroundings
Unit Cell = a collection of 3 vectors along Crystallographic axes each of which is described by a magnitude or length and an angle from the origin. These 6 parameters (3 magnitudes and 3 directions) are the Lattice parameters.
There are several ways to categorize crystals. One involves the 7 crystal systems described on pp. 35 of the text. The crystal systems are described in terms of the Lattice parameters.
Cubic a=b=c a=b=g=90° S, FC, BC
Tetragonal a=b a=b=g=90° S, BC
Orthorhombic a=b=g=90° S, FC, BC, BaseC
Rhombohedral (Trigonal) a=b=c a=b=g=Not 90° S
Hexagonal a=b a=b =90° g=120° S
Monoclinic a=b =90° S, BaseC
Triclinic S
Primitive Cell (Simple above) = One Lattice Point per cell
Non-Primitive = More than one point per cell
Points per cell = N = Ninterior + Nface/2 + Ncorner/8 + Nedge/4
Figure 2-3 shows Unit Cells.
In addition to classification according to Lattice Parameters, crystal structures can be classified according to symmetry operations that can be performed on them. There are 4 symmetry operations:
Reflection
Rotation
Inversion
Rotation/Inversion
Figure 2-6 shows symmetry elements for a cube with some of the symbols associated with these operations.
Symmetry operations were used to choose the 7 crystal systems above.
A combination of symmetry operations and translations are used to construct crystal systems. There are 3 translations commonly used,
Body Centering
Face Centering
Base Centering
Lattice Directions and Planes
It is important to remember the standard use of brackets in crystallography:
[u,v,w] is a direction (Square brackets)
a bar over u, v or w indicates a negative direction
<uvw> are directions of a form (pointy brackets) this is a class of similar directions
<111>
[111],[111],[111],[111]
(hkl) are the miller indices for a plane. h,k,l are fractional intercepts, 1/u, 1/v, 1/w of a plane with the a,b,c axies. Actual intercept is a/u, b/v, c/w, Miller indices are fractional intercepts, i. e. intercept divided by magnitude of a, b, c.
Atomic size and Coordination
XRD is a primary means to determine atomic sizes and coordination. Typically, a spherical model is used for simple atoms. For space filling spheres in a HCP lattice c/a = 1.633, (occupied volume =74%).
For typical metals c/a is 1.58 (Beryllium) 1.89 Cadmium. This is interpreted as non-spherical atoms. Atoms must be ellipsoidal. This is part of how atoms "choose" a crystal system.
For BCC (a-Iron) the closest approach is along the [111] direction, BCC closest approach = aÃ3/2 = 0.866 a.
For FCC closest approach is Ã2/2 a = 0.707 a.
For HCP closest approach in hexagonal plane is a
between atoms in hexagonal plane and next hexagonal plane closest approach is
Ã(a2/3 + c2/4)
From these equations applied to atoms in different crystal structures several things can be said,
1) atomic size remains fairly constant in different crystalline structures
2) atomic size has a fairly predictable change with coordination number (number of nearest neighbors)
CRYSTAL Coordination Number
FCC or HCP 12
BCC 8
Diamond Cubic 4
In this series diameter decreases by about 3% from FCC/HCP to BCC and by about 9% from BCC to Diamond Cubic.
Atomic size also changes slightly with the type of bonding (ionic, covalent, metallic, van der Waals)
Chain Folding:
The planar zigzag of the olefin or PE molecule crystallize as shown above into an orthogonal unit cell. This unit cell can be termed the first or primary level of structure for the olefin crystal. Consider a metal crystal such as the FCC structure of copper. The copper atoms diffuse to the closest packed crystal planes and the crystal grows in 3-dimensions along low-index crystal faces until some kinetic feature interferes with growth. In a pure melt with low thermal quench and careful control over the growth front through removal of the growing crystal from the melt, a single crystal can be formed. Generally, for a metal crystal there is no particular limitation which would lead to asymmetric growth of the crystallite and fairly symmetric crystals result.
This should be compared with the growth of helical structures such as linear oligomeric olefins, figure 4.1 on pp. 143 of Strobl. Here there is a natural limitation of growth in the c-axis direction due to finite chain length. This leads to a strongly preferred c-axis thickness for these oligomers which increases with chain length. In fact, a trace of chain length versus crystallite thickness is a jagged curve due to the differing arrangement of odd and even olefins, but the general progression is linear towards thicker crystals for longer chains until about 100 mer units where the curve plateaus out at a maximum value for a given quench depth. (Quench depth is the difference between the equilibrium melting point for a perfect crystal and the temperature at which the material is crystallized.)
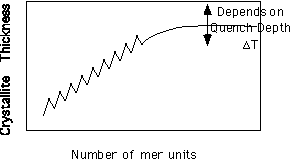
Schematic of olefin crystallite thickness as a function of the chain length.
The point in the curve where the crystallite thickness reaches a plateau value in molecular weight is close to the molecular weight where chains begin to entangle with each other in the melt and there is some association between these two phenomena. Also, the fact that this plateau thickness has a strong inverse quench depth dependence suggests that there is some entropic feature to this behavior (pp. 163 eqn. 4.20 where dc is the crystallite thickness and pp. 164 figure 4.18 Strobl).
Considering a random model for chain structure such as shown in figure 2.5 on pp. 21 as well as the rotational isomeric state model for formation of the planar zigzag structure in PE, pp. 15 figure 2.2, it should be clear that entropy favors some bending of the rigid linear structure, and that this is allowed, with some energy penalty associated with gauche conformation of figure 2.2. Put another way, for chains of a certain length (Close to the entanglement molecular weight) there is a high-statistical probability that the chains will bend even below the crystallization temperature where the planar zigzag conformation is preferred for PE. When chains bend there is a local free energy penalty which must be paid and this can be included in a free energy balance in terms of a fold-surface energy if it is considered that these bends are locally confined to the crystallite surface as shown on pp. 161 figure 4.15; and pp. 185 figure 4.34.
There are many different crystalline structures which can be formed under different processing conditions for semi-crystalline polymers (Figures 4.2- 4.7 pp. 145 to 149; figure 4.13 pp. 157; Figure 4.19, pp. 165; figure 4.21 pp. 170). As a class these variable crystalline forms have only two universal characteristics:
This means that understanding the relationship between quench depth and crystallite thickness is one of only two concrete features for polymer crystals. John (Jack) Hoffman was the first to describe this relationship although his derivation of a crystallite thickness law borrowed heavily on asymmetric growth models form low molecular weight, particularly ceramic an metallurgical systems. Hoffman's law is given in equation 4.23 on pp. 166:
![]() , Hoffman Law
, Hoffman Law
where n* is the thickness of the equilibrium crystal crystallized at T (which is below the equilibrium melting point for a crystal of infinite thickness, Tf°), s is the excess surface free energy associated with folded chains at the lateral surface of platelet crystals, and DH is the heat of fusion associated with one monomer.
Hoffman's law can be obtained very quickly for a free energy balance following the "Gibbs-Thomson Approach" (Strobl pp. 166) if on considers that the crystals will form asymmetrically due to entropically required chain folds and that the surface energy for the fold surface is much higher than that for the c-axis sides..
At the equilibrium melting point DG° = 0 = DH - T° DS, so DS = DH/ T°.
At some temperature, T, below the equilibrium melting point, The volumetric change in free energy for crystallization DfT = DH - T DS = DH(1 - T/T°) = DH(T° - T)/ T°.
The crystallite crystallized at "T" is in equilibrium with its melt and this equilibrium state is adjusted by adjusting the thickness of the crystallite using the surface energy, that is,
D
GT = 4Rt sside+ 2R2 s - R2t DfT = 0 at T.That is, At T the crystallite of thickness "t" is in equilibrium with its melt and this equilibrium is determined by the asymmetry of the crystallite, t/R. If
DfT = DH(T° - T)/ T°. is use in this expression,4t
sside+ 2R s = R t DH(T° - T)/ T°.Assuming that
sside <<< s, and "t"<<<"R" then,t = 2
s T°./( DH(T° - T))which is the Hoffman law.
The deeper the quench, (T° - T), the thinner the crystal and for a crystal crystallized at T°, the crystallite is of infinite thickness. (Crystallization does not occur at T°).
Hoffman-Weeks Plots for T°
It becomes important to determine certain parameters in the Hoffman approach, first some estimate of
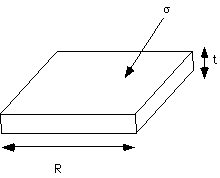
s is desired and this has been done using the rotational isomeric state model among other methods. The values which have been obtained (mostly by Hoffman and Keller) seem to agree with crystal thickness measurements.Second, a determination of T° is critically important. This can be obtained through the Hoffman-Weeks plot which is based on the above theory.
The simplest way to estimate T° is a plot of the melting point, Tm, for crystals whose thickness is known from other measurements such as SEM or small angle x-ray scattering (SAXS). Such a plot will be linear if the Hoffman theory is followed.
This method requires extensive measurements of crystal thickness as well as measurement of the melting point.
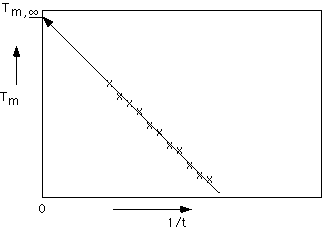
Hoffman-Weeks theory is based on the difference between melting, Tm, and crystallization , Tc, temperatures. In the Hoffman-Weeks approach, it is considered that any crystallite formed at temperatures less than T° has some imperfections "locked-in". Generally, the melting temperature is higher than the crystallization temperature, Tm>Tc. Hoffman and Weeks defined a stabilization parameter,
f', which is zero for crystallites with no imperfections and has a value of 1 for an unstable crystal with all imperfections. For the most stable crystallite Tm = T°. For the completely unstable crystallite, Tm = Tc. For a typical crystallite, f'=1/2. Using a simple weighting law, Hoffman and Weeks wrote a linear expression relating Tm, T° and Tc,Tm = T°(1-
f') + f' TcThis linear law implies plots of Tm versus Tc to obtain T° without requiring a measurement of the crystallite thickness. At T° , Tm = Tc = T° according to this approach. The Hoffman-Weeks approach and the more direct approach yield very close values for T°.
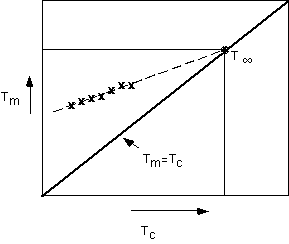
Hoffman-Weeks plot for T°.
Nature of the Chain Fold Surface:
In addition to determination of T°, the specific nature of the lamellar interface in terms of molecular conformation is of critical importance to the Hoffman analysis. There are several limiting examples, 1) Regular Adjacent Reentry, 2) Switchboard Model (Non-Adjacent Reentry), 3) Irregular Adjacent Reentry (Thickness of interfacial layer is proportional to the temperature).
The synoptic or comprehensive model involves interconnection between neighboring lamellae through a combination of adjacent and Switchboard models.
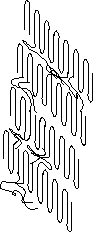
The interzonal model involves non-adjacent reentry but considers a region at the interface where the chains are not randomly arranged, effectively creating a three phase system, crystalline, amorphous and interzonal.
Several distinguishing features of the lamellar interfaces are characteristic of each of these models.
Adjacent Uniform and Thin Fold Surface High Surface Energy
Switchboard Random chains at interface, Broad interface, Low Surface Energy
Irregular Adjacent Temperature Dependent interfacial thickness Intermediate Surface Energy
Interzonal Extremely Broad and diffuse interfaces with non-random interfacial chains
Synoptic Interfacial properties are variable depending on state of entanglement and speed of crystallization.
The Hoffman equation states that the lamellar thickness is proportional to the interfacial energy so we can say that Adjacent reentry favors thicker lamellae since adjacent reentry has the highest interfacial energy and the more random interfacial regions should display thinner lamellae.
When polymers crystallize from a relatively dilute solution it is expected that Regular Adjacent Reentry is a strong possibility. When crystallization occurs from a melt, where entanglements dominate, a switchboard reentry or synoptic model is expected. The differences between these interfacial conformations will have important consequences for the lamellar thickness since thickness should be proportional to the interfacial energy for the fold surface.
The nature of the fold surface has been the most debated topic in polymer crystallography. Chiefly, Hoffman, Keller and workers at the National Institute of Standards and Technology have pushed the idea of adjacent reentry as the primary mechanism. This has recently been supported by atomic force micrographs of adjacent reentry from melt crystallized PE by Abe at the University of Akron. Proponents of the switchboard model have included Paul Flory and Fischer in Germany. Strobl is clearly in favor of less ordered reentry models in our text book and this should be taken with a grain of salt. Clearly, the nature of the lamellar interface will vary depending on a variety of conditions such as the polymer concentration, state of entanglement, rate of crystallization, molecular weight and other factors. Under ideal conditions where transport is not particularly important adjacent reentry probably dominates and there is fairly strong evidence for this from the NIST groups. In processed materials where crystallization rates are fast and molecular weights are high, the synoptic model is probably more appropriate.
Strobl discusses several studies which point to the existence of a fairly wide interlamellar region consistent with the synoptic model. Figure 4.26 shows Raman spectroscopy data where there is an identifiable "transition" or interlamellar band. Transforms of small-angle-x-ray scattering data show a broad interlamellar region for some samples (figure 4.28) and 2-d, solid state NMR data shown in figure 4.35 supports correlations between amorphous and crystalline regions indicating a fairly broad transition region. Much of the evidence presented by Strobl falls in the category of a selective view of the interfacial region and reflects the deep divides in the field between adjacent reentry camps and groups which support a more random model.
A notable theoretical addition to these arguments is the so called "Gambler's Ruin" Model of Edward diMarzio (NIST) which basically lead to the development of the Interzonal model from the Flory camps. di Marzio proved in the Gambler's Ruin papers (Macromolecules circa 1985-90) that the switchboard model is not possible basically due to density constraints. That is, it can be proven that a completely random amorphous phase can not directly connect to a completely crystalline phase at the chain ends as in the switchboard model since this would require dramatic and unnatural densities in the interzonal region. Such unnatural densities (in fact a vacuum would be created) have never been observed experimentally. The NIST camp considered these papers theoretical proof for adjacent reentry. By this time Flory himself was dead and his group of workers fairly dispersed. The interzonal model which allowed for ordering in the interlamellar region was a solution to the Gambler's ruin theory proposed in concept by di Marzio. (di Marzio is also known for his seminal work in glass transition theory and in polymer miscibility among other contributions.)
Colloidal Scale Structure in Semi-Crystalline Polymers:
Lamellae crystallized in dilute solution by precipitation can form pyramid shaped crystallites which are essentially single lamellar crystals (figure 4.21 for example). Pyramids form due to chain tilt in the lamellae which leads to a strained crystal if growth proceeds in 2 dimensions only. In some cases these lamellae (which have an aspect ratio similar to a sheet of paper) can stack although this is usually a weak feature in solution crystallized polymers.
Lamellae crystallized from a melt show a dramatically different colloidal morphology as shown in figure 4.30 pp. 182, 4.13 on pp. 157, 4.7 on pp. 149, 4.6 on pp. 148, 4.4 and 4.5 on pp. 147 and 4.2 on pp. 145. In these micrographs the lamellae tend to stack into fibrillar structures. The stacking period is usually extremely regular and this period is called the long period of the crystallites.
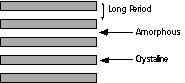
The long period is so regular that diffraction occurs from regularly spaced lamellae at very small angles using x-rays. Small-angle x-ray scattering is a primary technique to describe the colloidal scale structure of such stacked lamellae. The lamellae are 2-d objects so a small angle pattern is multiplied by q2 to remove this dimensionality (Lorentzian correction) and the peak position in q is measured, q*. q= 4
p/l sin(q/2), where q is the scattering angle. Bragg's law can be used to determine the long period, L = 2p/q*. Figure 4.8 on pp. 151 shows such Lorentzian corrected data. The peak occurs at about 0.2 degrees! In some cases the x-ray data has been Fourier transformed to obtain a correlation function for the lamellae which indicate an average lamellar profile as shown in figure 4.9 pp. 152.The degree of stacking of lamellae would appear to be a direct function of the density of crystallization, i.e. in lower crystallinity systems stacking is less prominent, and the extent of entanglement of the polymer chains in the melt. You can think of lamellar stacking as resulting from a reeling in of the lamellae as chains which bridge different lamellae further crystallize as well as a consequence of spatial constraints in densely crystallized systems.
In melt crystallized systems, many lamellar stacks tend to nucleate from a single nucleation site and grow radially out until they impinge on other lamellar stacks growing from other nucleation sites. The lamellar stacks have a dominant direction of growth, that is, they are laterally constrained in extent, so that they form ribbon like fibers. The lateral constraint in melt crystallized polymers is primarily a consequence of exclusion of impurities from the growing crystallites.
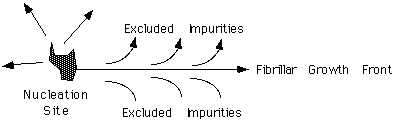
"Impurities" include a number of things such as dirt, dust, chain segments of improper tacticity, branched segments, end-groups and other chain features which can not crystallize at the temperature of crystallization. Some of these "Impurities" will crystallize at a lower temperature so it is possible to have secondary crystallization occur in the interfibrillar region. Despite the complexity of the "impurities" it can be postulated that the impurities display an average diffusion constant, D. The Fibrillar growth front displays a linear growth rate, G. Ficks first law states that the flux of a material, J, is equal to the negative of the diffusion constant times the concentration gradient
Dc/Dx. If we make an association between the flux of impurities and the growth rate of the fibril then Fick's first law can be used to associate a size scale, Dx with the ratio of D/G. This approach can be used to define a parameter d, which is known as the Keith and Padden d-parameter, d = D/G. This rule implies that faster growth rate will lead to narrower fibrils. Also, the inclusion of high molecular weight impurities, which have a high diffusion constant, D, leads to wider fibrils. There is extensive, albeit qualitative, data supporting the Keith and Padden del parameter approach to describe the coarseness of spherulitic growth in this respect.Branching of Fibrils: Dendrites versus Spherulites.
Low molecular weight materials such as water can grow in dendrite crystalline habits which in someway resemble polymer spherulites (collections of fibrillar crystallites which emerge from a nucleation site). One major qualitative difference is that dendritic crystalline habits are very loose structures while spherulitic structures, such as shown in Strobl, fill space in dense branching. At first this difference might seem to be qualitative.
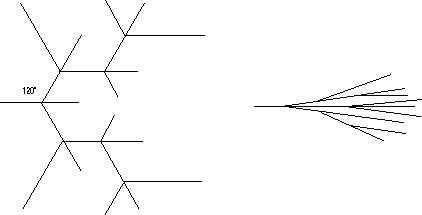
In low-molecular weight materials such as snowflakes or ice crystallites branching always occurs along low index crystallographic planes (low Miller indices). In spherulitic growth there is no relationship between the crystallographic planes and the direction of branching. It has been proposed that this may be related to twinning phenomena or to epitaxial nucleation of a new lamellar crystallite on the surface of an existing lamellae. A definitive reason for non-crystallographic branching in polymer spherulites has not been determined but it remains a distinguishing feature between spherulites and dendrites.
(Incidentally, the growth of dendrites can occur due to similar impurity transport issues as the growth of fibrillar habits in polymers. In some cases a similar mechanism has been proposed where rather than impurity diffusion, the asymmetric growth is caused by thermal transport as heat is built up following the arrows in the diagram on the previous page.)
Non-crystallographic branching leads to the extremely dense fibrillar growth seen in figures 4.4 to 4.7 of Strobl. In the absence of non-crystallographic branching, many of the mechanical properties of semi-crystalline polymers would not be possible. As was mentioned above, non-crystallographic branching may be related to the high asymmetry and the associated high surface area of the chain fold surface which serves as a likely site for nucleation of new lamellae as will be discussed in detail below in the context of Hoffman/Lauritzen theory.
The formation of polymer spherulites requires two essential features as detailed by Keith and Padden in 1964 from a wide range of micrographic studies:
Polymer Spherulites.
Figure 4.2 pp. 145 shows a typical melt crystallize spherulitic structure which forms in most semi-crystalline polymeric systems. The micrographs in figure 4.2 are taken between crossed polars and the characteristic Maltese Cross is observed and described on the following page. The Maltese cross is an indication of radial symmetry to the lamellae in the spherulite, supporting fibrillar growth, low angle branching and nucleation at the center of the spherulite. In some systems, especially blends of non-crystallizable and crystallizable polymers, extremely repetitive banding is observed in spherulites as a strong feature, figure 4.7 pp. 149. Banding is especially prominent in tactic/atactic blends of polyesters and it is in these systems in which it has been most studied. It has been proposed by Keith that banding is related to regular twisting of lamellar bundles in the spherulite (circa 1980). Keith has proposed that this twisting is induced by surface tension in the fold surface caused by chain tilt in the lamellae (circa 1989). Since most spherulites crystallize in an extremely dense manner it has been difficult to support Keith's hypothesis with experimental data. Regular banding has, apparently, no consequences for the mechanical properties of semi-crystalline polymers so has been essentially ignored in recent literature.
Spherulitic Growth Rate versus Quench Depth.
By careful observation in an optical microscope it is possible to measure the linear growth rate of spherulitic crystals in a polymer at various quench depths (
DT = T° - Tc). At low undercoolings the growth rate is slow since the thermodynamic driving force for crystallization is low. As the quench depth is increased the growth rate increases, reaches a maximum at about 50° below T° and then monotonically decays with quench depth. This type behavior is shown in figure 4.16 pp. 162 and is characteristic of many materials. Similar curves can be obtained by careful thermal analysis.u (T) = k (Transport (T)) (Growth driving force (T))
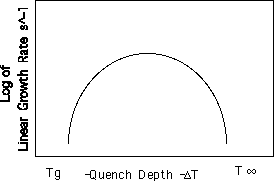
The left size of the plot of growth rated versus quench depth is governed by transport through an exponential function for the diffusion coefficient,
D = k e-
DF*/RTwhere
DF* is a negative activation barrier for thermal transport which could be based on free volume concepts for instance. In systems which display a glass transition temperature this exponential will follow the Vogel-Fulcher or WLF dependence which Strobl gives as equation 4.17 pp. 162,Flux Å k exp(-TA/(T - TV))
Where TA is an activation temperature (1000-2000°K) and TV is related to the glass transition temperature (usually somewhat lower than the measured Tg).
The thermodynamic driving force for crystallization was given above as
DfT = DH(T° - T)/ T°., which yields a rate law proportional to exp(-B/( T° - T)). On the bottom of pp. 162 Strobl gives equation 4.19 which predicts the thermal dependence of linear growth rate,u Å exp(-TA/(T-TV)) exp(-B/( T° - T))
This equation is symmetric about a maximum since both exponential terms have similar form.
Lamellar growth in polymer crystals has several features which distinguish it from crystalline growth in low molecular weight materials. First, the highest surface energy surface, (fold surface) is not the surface of maximum growth since the chains are not in the proper helical form at this interface by definition. In low-molecular weight materials, secondary nucleation rates and substrate completion rates are comparable. This is not always the case for polymer crystals and this fact has lead to the development of a regime approach to describe the linear growth rate of polymer lamellae.
Hoffman-Lauritzen Theory for Linear Growth Rate (1973):
The figure below shows a schematic of the two competing factors which govern the linear rate of crystallization for a polymer lamellar crystal. The direction of crystal growth is up. The rate of this linear growth, u, is governed by the rate of nucleation (secondary nucleation) on the lateral surface of the growing lamellae, i, and the rate of completion of the substrate layer, g.
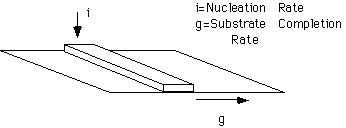
From the relative magnitudes of "i" and "g" Hoffman predicted several regimes of crystalline growth for spherulitic polymers. Hoffman defined three basic regimes:
Regime I: i<<g, this is nucleation dominated secondary crystalline growth.
Regime II: i Å g, Two rates are comparable.
Regime III: i>>g, Many nuclei lead to disordered crystal growth.
These three regimes of growth, defined by Hoffman, will be discussed in some detail as they form the basis for much of the current literature in polymer crystallization.
Regime I Growth: (Shallow quench => Axialites)
i<<g
In regime I a single surface nucleus forms which is called a "Stem". The linear growth rate, GI, depends on the rate of deposition of stems, "i",
GI = b0 i L = b0 a0 ns i
a0 is the chain width, b0 is the layer thickness, i.e. the lamellar crystallite thickness, t, ns is the number of stems in a layer. The assumption being that when one stem is nucleated the entire layer of nS stems is almost immediately completed relative to the nucleation rate, i. The length of a layer is L = a0 nS.
The rate of deposition of the stem, i, depends on the transport of a stem to the surface and the nucleation constant, KG(I),
GI = CI exp(-Q*D/RT) exp(+K G(I)/T(
DT))where Q*D is the activation energy for reptation of the chain to the crystalline surface. CI is inversely related to molecular weight.
Regime II Growth: (Deep quench => Spherulites)
In Regime II Multiple surface nuclei form since i Å g. The growth rate is given by,
GII = b0 (2 i g)1/2
The separation distance for stems is given by the ratio of g to i (g can occur in two directions),
Sn = 1/Nk = (2g/i)1/2
where Nk is the number of stems per distance.
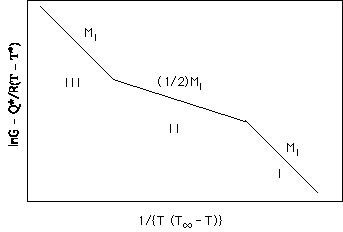
Regime II is the normal condition for spherulitic growth. It has a weaker
DT dependence than regime I.lnGII Å 1/2 ln GI
The latter gives a signature of regime I to regime II transition and has been used as evidence for the validity of the Hoffman approach.
Regime III Growth: (Very deep quench => distorted spherulitic like structures)
In regime III, Sk goes to a0! i>>g, the surface is completed by nuclei with little growth along the surface. The growth rate is given by,
GIII = b0 i L = b0 i nS a0
In regime III there are certainly few chain folds.
The log of GIII has the same slope in log temperature as that of GI and these slopes are used as an indicator of these regime transitions as discussed below.
Morphological Consequences of the Regime Approach:
The regime approach can be used as a tool to qualitatively consider morphological changes which have been observed with quench depth.
In Regime I, substrate completion is a slow and ordered process which allows time for transport of chains to the growing surface. It is qualitatively expected that chain folding will be of the adjacent reentry type in such a slow, controlled process. This means that lamellae will, most likely, have few synoptic connections which are necessary for well stacked lamellae and a fibrous growth motif. Additionally, the absence of tie chains between lamellae might be expected to hinder significant epitaxial nucleation, interfering with low-angle, non-crystallographic branching. For these reasons it might be expected that Regime I growth would not lead to good spherulitic growth and this is strongly supported by microscopic observation.
In Regime II, crystallization occurs with some synoptic connections between lamellae since a multiple seeding situation necessarily leads to dangling chains where growth fronts meet. These connections ensure that lamellae will be well stacked and offer and opportunity for epitaxial nucleation and extensive low-angle branching required for good spherulitic growth.
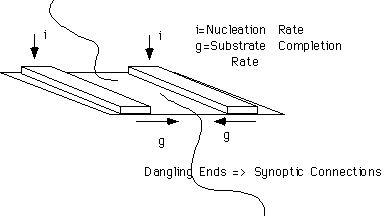
In Regime III, substrate completion is dominated by nucleation events and few regular chain folds occur. Lamellae are disorganized and have many defects under these conditions. This leads to distorted crystalline structures which do not produce good spherulitic structures.
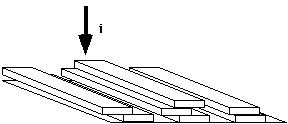
Growth Rate Signature of the three Regimes:
Hoffman described an approach whereby the three growth regimes could be distinguished from growth rate versus isothermal crystallization temperature data. He first wrote a generic equation for the linear growth rate which included a transport term (later based on reptation) and a free energy term:
![]()
where the first exponential is a transport term and the second exponential is a thermodynamic growth rate term. Taking the logarithm of both sides of this equation suggests a plotting scheme if the transport term can be measured in an independent experiment,
![]()
Plots of the log of growth rate minus the transport constant (which can be independently determined) versus 1/T(T° -T) will yield the growth constant Kg. For Regime I, Kg is proportional to ln(i), for Regime II, to 1/2 ln(i) and for Regime III, to ln(i) since g is proportional to i in all cases. The slope of this reduced growth rate curve will be the same in Regime I and Regime III but will be 1/2 of the Regime I slope in Regime II. The prefactor is different for the three regimes,
Problems with Regime Approach:
1) The Regime theory predicts rather sharp transitions between the growth rate in different regimes yet data shows more gradual transitions.
2) It is difficult to observe regimes since: a) Crystallization is too slow in Regimes I and III, deep quenches are difficult to achieve instantaneously, i.e. without going through some crystallization in Regime II, Rate of crystallization is very slow in Regime I (and III).
3) The analysis shown in the graph above relies on a good knowledge of the transport term and its temperature dependence. There is debate over the proper values to use for this transport term as it involve polymer self-diffusion which is difficult to measure.
Avrami Analysis for Spherulitic Growth Rate:
The rate of phase growth in most systems typically follows a scaled exponential rate law which was first proposed by Avrami. A scaled exponential rate law is exponential of time raised to some (usually non-integral) power. The Avrami equation is quite general for growth of phases, and has been adopted to describe spherulitic growth in polymers. Strobl shows a number of exponential growth curves in figure 4.14 on pp. 159, a schematic of which is shown below,

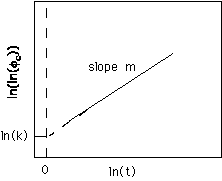
The Avrami Equation is given by,
f
c(t) =1 - exp(-ktm) Strobl equation 4.15 pp. 160The parameter "k" and the power "m" can be calculated for certain model conditions of growth. The Avrami plot involves a double log/log plot of volume fraction versus time,
ln(ln fc(t)) = m ln(t) + ln k
and results in a linear plot of slope m and extrapolated intercept ln(k).
The Avrami approach is based on two assumptions:
1) Growth is linear in time and a constant linear growth rate is observed, dr/dt.
2) Growth is diffusion limited rather than nucleation limited.
There are two main choices which determine the Avrami parameters "m" and "k" under these assumptions.
1) Is nucleation spontaneous (growth all starts at the same time, number of nuclei = N) or sporadic (growth starts at a constant rate, dN/dt)
2) What is the dimension of growth, 1-d like a fiber or rod, 2-d like a disk or platelet, 3-d spherical growth.
Consider a condition of spontaneous nucleation, N nuclei, with 2-d growth at a rate dr/dt. Growth
fronts travel a distance rt = t dr/dt in time t. Consider a point x in the nucleating bath. The average number of growth fronts which cross point "x" at time "t", <F> is the area fraction of the disk phase, N Ac where N is now the number per area of nucleation sites and Ac is the area of one disk phase. This is given by,
<F> = N p (rt)2 = N p (t dr/dt)2
The number of growth fronts which cross the point x can be described by a Poisson distribution since the crossing of "x" is a random phenomena for randomly placed nuclei,
p(F) = exp(-<F>) <F>F/F!
This function describes the probability that a certain number of fronts have crossed a point x, i.e. the probability for F = 0 is the probability that no fronts have crossed or the probability that the point x is amorphous in this case. p(F=0) can then be related to the amorphous fraction or 1 - fc,
p(F=0) = exp(-<F>) = (1 - fc)
The expression for <F> can now be used to determine "m" and "k" for this condition,
f
c = 1 - exp(-N p (t dr/dt)2)The Avrami exponent, m = 2 for spontaneous nucleation of 2-d domains. For 1-d domains the exponent is 1 and for 3-d domains the exponent is 3. The constant k = N
p (dr/dt)2 for 2-d growth and analogous expressions can be obtained for other dimensional growths.For sporadic nucleation, at a rate dN/dt, a similar approach can be used. Consider a differential ring of thickness dr around the point x, considered previously, at a distance r from x. The differential number of fronts crossing x at time t, dF, is given by
dF("t" or "r") = (Area of the "dr" ring) (area fraction rate of nuclei production) (Differential time span associated with "dr")
= (2
prdr) (dN/dt) (t - r/(dr/dt))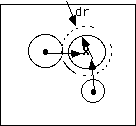
The average number of fronts which cross x at time "t" is given by,
![]()
This means that m = 3 for sporadic nucleation and 2-d growth and k =
p (dN/dt) (dr/dt)2/3. Sporadic nucleation adds one to the Avrami exponent for the dimensional cases listed above.There are many problems with the Avrami analysis and a few of these are listed below,
1) It is difficult to distinguish between dimensional effects and nucleation type effects. Often systems are much more complicated than the models discussed above.
2) Non-integral Avrami exponents are the norm and these do not have a simple explanation.
3) Any thing looks linear in a log-log plot over a narrow range and a double log plot is even worse.
4) Power-law analysis requires a significant range of t (many decades) which are not available in almost any real cases.
5) Strobl notes some other deficiencies on pp. 160.
=>Back To Characterization Lab
Download this page: =>Semmi-Crystalline Morphology.pdf