=>Back To Characterization Lab
Download this page: =>Phase Behavior.pdf
4 Phase Behavior of Amorphous Polymer Systems.
Chapter 3, Section 3.2, 3.3 pp. 83-141
General Issues:
Flory Huggins equation for the Gibbs Free Energy of Mixing, DG is given by,
![]()
Equation 3.85 and 3.86 pp. 88 Strobl. fi is the volume fraction of component "i", Ni is the degree of polymerization, c is the Flory Huggins interaction parameter. The first two terms represent the combinatorial entropy of mixing while the latter term represents the enthalpic component of the free energy change on mixing which should reflect only local site-site interactions of neighboring mer units. The interaction parameter in this form is given by,
![]()
c
has an inverse temperature dependence and since this is the only place in the free energy change expression where temperature is involved the thermal dependence of miscibility can be written in terms of c or T. The first derivative of free energy with respect to composition reflects the condition of equilibrium through equality of chemical potentials between coexisting phases. The second derivative reflects the condition for stability (spinodal) of a system to small perturbations in composition and the third derivative reflects the critical point for miscibility. From these thermodynamic definitions the critical point for a polymer mixture and the spinodal curve in composition can be obtained. The critical point occurs at fc and at a temperature reflected in cc,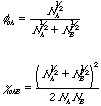
The spinodal curve for the Flory-Huggins equation is defined as,
![]()
Figure 3.14 (pp. 91) shows the calculated Free energy change on mixing for a symmetric blend, NA = NB, as predicted by the Flory Huggins equation. The above equations show that the critical composition for this situation is 0.5 and the critical cc is 2/N. Because of this dependence of the critical interaction parameter on molecular weight, N, physicists often plot cN versus composition rather than T versus composition in constructing a phase diagram for a polymer system, lending some degree of universality to the plots.
In Figure 3.14, the free energy change on mixing shows three behaviors which are reflected in the three derivatives discussed above. At low c (high temperatures), there is a single minimum reflecting miscibility. At the critical c, cN = 2, the curve becomes markedly flat associated with a transition to a double minima curve at lower temperatures. At large c (low temperature), two minima in the free energy change are observed. The bottom curve represents a single phase system, the middle curve represents a critical system having a temperature just at which phase separation begins while the upper curve represents a system where phase separation will occur, the two phases which form corresponding in composition to the points where a line is tangent to both curves. The points of tangent are the binodal points at that temperature. Another pair of points, where the free energy change goes from concave down to concave up reflects the stability limit where spontaneous decomposition occurs.
Figure 3.15 on pp. 93 shows these two sets of points for various cN as a function of composition. The critical point is where all of these derived curves meet. In this case the critical point, which defines the limit of phase miscibility, occurs at a low temperature similar to low molecular weight systems, i.e. you heat sugar to dissolve it in water. Often polymer systems display the opposite behavior, phase separation on heating (PVME/PS system). From an empirical perspective such behavior necessarily involves a major modification of the definition of the interaction parameter.
The definition of c, above, is of the form B/T reflecting the enthalpic nature of this parameter. From the Flory-Huggins equation this can lead only to systems which phase separate on cooling (upper critical solution temperature, UCST, systems, figure 3.17 pp. 96) or systems which are always single phase (for negative B). In order to obtain phase separation on heating (LCST systems which are commonly observed in polymers), there must be a negative B and a positive temperature independent term, A, in c which reflects an entropic component, c = A + B/T, figure 3.18 pp. 97. Such an entropic component of c is termed a non-combinatorial entropy reflecting the combinatorial (counting) statistics used in the derivation of the Flory-Huggins equation.
Morphology of Phase Separation in Polymer Blends:
A LCST phase diagram is shown below:
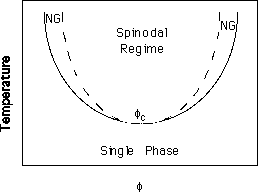
A quench into the spinodal regime (in this case raising the temperature of the system) leads to spontaneous decomposition into two phases following concentration fluctuations in the system. A quench into the nucleation and growth regime (NG) will only lead to phase separated structures in the presence of nuclei for phase growth (dirt). The growth will occur locally at these nucleation sites and will lead to spherical domains. The two situations are shown by Strobl in figure 3.21 on pp. 101. A single phase present in the spinodal regime is unstable to small concentration fluctuations. A single phase present in the binodal (NG) regime is meta-stable to small concentration fluctuations but unstable to large concentration fluctuations such as presented by a nucleation site.
A common way to look at the difference between spinodal decomposition and nucleation and growth is to consider concentration for the system versus spatial arrangement, figure 3.24 pp. 104. In nucleation and growth the nuclei is thermodynamically stable and represents a concentrated region. The phase of which the nuclei is rich is depleted from the local vicinity of the phase to produce growth in the phase. This depletion leads to Fickian (normal) diffusion down a concentration gradient.
For spinodal decomposition the thermodynamic driving force is sufficient to force upward diffusion so that any concentration fluctuation, no matter how small, will grow by transport up the concentration gradient. This situation was first realized by Cahn and Hilliard in the 1950's.
Critical Fluctuations and Spinodal Decomposition:
A single phase system such as a blend of two polymers contains fluctuations in concentration due to random thermal motion of the blend components. (Some of these fluctuations are larger than others, particularly near the average coil size in the mixture.) Thermal fluctuations are dampened by the nature of the free energy curve discussed above. For example, consider an average concentration <f> = 0.25 system where small thermal fluctuations exist as shown below,
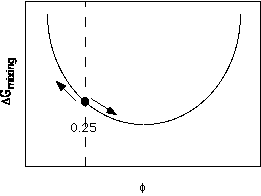
A thermal fluctuation away from the average composition leads to two phases as indicated by the arrows, which have a net higher free energy since the increasing free energy is much steeper than the decreasing free energy. This means that the free energy dampens thermal fluctuations when deep in the single phase regime.
As one approaches the critical point the free energy curve flattens out, especially in the vicinity of the critical composition so this damping effect is less pronounced and at the critical point and critical composition there is no damping at all. This means that concentration fluctuations grow as one approaches the critical point.
Scattering of radiation (light, x-rays or neutrons) arises from concentration (contrast) fluctuations,
S(q) = <dfq2>/Vc,
where S(q) is proportional to the scattered intensity, Vc is a lattice volume element from the Flory-Huggins approach for instance, and dfq is the q wave vector component of the difference between a concentration value and the mean concentration in the system,
df
q = fq - <f><
dfq> = 0. fq involves breaking up essentially random thermal concentration fluctuations into Fourier components (a series of cosine waves). Fourier theory is based on the assumption that these Fourier components can be treated independently. For a single Gaussian polymer coil <dfq2>/Vc can be calculated from the Gaussian statistics function leading to the Debye scattering function for a single polymer coil,![]()
where Q = q2Nb2/6 = q2Rg2, Rg is the radius of gyration for the polymer coil and q is the wavenumber for concentration fluctuations measured in the scattering experiment as = 4p/l sin(q), where l is the wavelength of the radiation and 2q is the scattering angle. q is also proportional to the inverse of the Bragg spacing, q = 2p/d.
The difference between scattering for light, x-rays and neutrons involves wavelength (size scale observed, light 0.6 Ám, neutrons 5 Å and x-rays 1.54Å), and contrast. Light is contrasted by polarizability or index of refraction, x-rays by electron density and neutrons by neutron cross section. Neutron cross-section is different for deuterium and hydrogen so polymer chains can be tagged by deuteration. Figure 3.26, pp. 107, demonstrates the enhancement of scattered intensity as the critical point is approached reflecting growth of concentration fluctuations. The typical plot is 1/Intensity (1/Sc) versus q2, reflecting the q2 dependence of the Debye function above. The divergence of the intensity extrapolated to q2 => 0 can be plotted as a function of 1/T to determine the critical point (or spinodal point for off critical compositions), figure 3.26 pp. 107.
The scattering function for a single phase polymer blend is similar to the Debye function and is described by an inverse sum of scattering functions and the interaction parameter by the Random Phase Approximation, equation 3.165, pp. 115, whose derivation is described in Strobl (Appendix).
![]()
The RPA equation above, describes the increase in 0-angle scattering SBlend(q=>0) as one approaches the critical point (or spinodal point). This function is commonly used to determine the value of the interaction parameter for single phase blends. At the q=>0 limit the RPA equation can be rewritten using the Flory-Huggins equation (for a symmetric blend) as,
![]()
Strobl equation 3.168 pp. 115, indicating that the deviation from the spinodal is directly measured in the extrapolated zero-angle intensity.
Spinodal Decomposition:
Beyond the critical point, within the spinodal regime, phase separation is spontaneous for all composition fluctuations. This is because of the shape of the free energy curve in the region as show below,
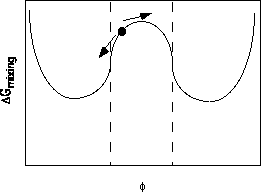
Any fluctuation away from the average concentration leads to a greater decrease in free energy for one of the two phases than the corresponding increase on the other side of the average concentration. This means that any concentration fluctuation leads to a lowering of the free energy. (in the nucleation and growth regime this is only true for very large concentration fluctuations which go beyond the central peak.)
Usually on a micron scale (light scattering) a peak is observed in the scattering for polymer systems under going spinodal decomposition. The peak reflects a "wave-like" fluctuation in the composition with a preferred wavelength. The existence of a peak in the scattering is shown in figures 3.27 and 3.28 for SANS and SALS data respectively. The peak grows indicating an increase in the concentration difference between phases as spinodal decomposition proceeds. In Cahn-Hillard theory, which predicts such a peak, the peak position remains constant in spinodally decomposing system and a bicontinuous, web-like structure is produced, figure 3.35 pp. 126. At late stages of spinodal decomposition the peak position decays in "q" reflecting an increase the phase size, q ┼ 1/d. This is termed late stage spinodal decomposition. At extremely late stages the web-like structure "ripens" into spherical domains due to surface energy in a process known as Oswald Ripening. The final product of Oswald Ripening is indistinguishable from the structure of a nucleation and growth process.
Spinodal decomposition also occurs for low molecular weight systems such as metals but on a much smaller size scale (nanometer scale) and at a much more rapid rate (seconds rather than minutes for polymers). Cahn-Hilliard theory was developed for metals but has its major application in polymers due to the difficulty of study of early stage spinodal decomposition in metals. For polymers both the time scale and size scale are extremely accessible for study and spinodal decomposition has been one of the major areas of interest to polymer morphologists.
To consider the growth of phases in the spinodal regime consider the free energy of a polymer blend of composition f, which contains small concentration fluctuations, G(f(r)), as described by the "Ginzburg-Landau Functional", Strobl equation 3.136 pp. 111 (and Hashimoto paper Macro 16, 641 equation II-1).
![]()
g(f(r)) is the free energy density as a function of concentration and phase size, r, and the second term contains the gradient of the concentration. The term b' reflects the cost associated with the presence of concentration fluctuations associated with df/dr (or del f in 3-d coordinates). This differs from a surface energy term since a "surface" does not exist, see figure 3.24 pp. 104.
The differential operator, del, has been used above. The divergence, del(Scalar), results in a vector composed of the derivative of the scalar with respect to the three Cartesian coordinates.
The Ginzburg-Landau Functional (function of arbitrary functions) simply states that the average free energy associated with the blend reflects the sum of component free energy densities times volume plus the average free energy associated with fluctuations. There is no linear term in del f because <df> = 0, so the second order term, <(df)2> is the simplest approximation. The expression should also include higher, even-powered terms for large concentration fluctuations. The term b' can be calculated for the specific system of interest, and for polymer blends it is given by,
![]()
so is associated with a natural size-scale for fluctuations in the system associated with the coil size (equation 3.163 pp. 114 and RTb"/2 = b', pp. 112 below 3.148). The value of b' is obtained by comparison of the Debye scattering function with the scattering function obtained from the Ginzburg-Landau Functional using Flory-Huggins Theory. (This is done by Strobl on pp. 113-114.)
The Ginzburg-Landau Functional introduces an expression for the variation of free energy with phase size, r.
In the study of phase separation we are dealing with the kinetic growth of phases so some kind of balance between thermodynamics, as described by the Ginzburg-Landau Functional, and transport from Fick's laws in tensor form, is needed. The growth of phases in spinodal decomposition is driven by the chemical potential difference between two regions of differing composition, i.e. the two phases. The flux of one binary blend component, A, JA (which also equals JB by incompressibility), is given by,
![]()
DAB is the translational diffusion coefficient for transport of A chains in an AB melt. This is a restatement of Fick's first law with the chemical potential difference replacing the concentration gradient (activity), Hashimoto above equation II-2. If the Ginzburg-Landau functional is used to calculate the chemical potential, then the expression for JA has a size dependence. Fick's second law can then be used to describe the rate of phase growth,
![]()
Hashimoto equation II-2. Here, the Ginzburg-Landau Functional has been used for the calculation of the chemical potential in the two phases, and this has been substituted in the expression for the change in concentration with time. The substitution of the Ginzburg-Landau expression implies a preferred size scale and a size-scale dependence to the growth of concentration. This is inherent to the above difference in the density gradient terms.
The differential operator, del, has been used above. The divergence, del(Scalar), results in a vector composed of the derivative of the scalar with respect to the three Cartesian coordinates. Higher order derivatives, del2 and del4 also result in a vector. The divergence of a vector field, del dot vector, results in a scalar which is the sum of the derivative of each vector component with respect to the Cartesian component axis. Del dot J, is a measure of the spatial change in flux from an infinitesimal volume element and is a measure of the deviation from steady state where in = out. This is therefore an equation of continuity.
The equation for concentration growth rate reflects a balance between the change in the chemical potential (second derivative of the free energy density) with respect to concentration, times the derivative of the concentration gradient in space, and a factor which accounts for the energy cost associated with a concentration gradient, b', in terms of an average size parameter for the system related to the radius of gyration for the component coils and the concentrations. The chemical potential is a bulk system parameter, i.e. reflects the largest size scales so that an infinite ensemble is an appropriate approximation. The parameter, b', indicates that the system contains some natural size-constant which you might view as being similar to a time-constant for a temporally oscillating system. i.e. here oscillations are in concentration rather than in time for something like a pendulum. This is basically what Strobl means by and "equation of motion" on the top of pp. 121. Depending on the relative values of the derivative of the chemical potential and the parameter b', the system will select certain "frequencies" in spatial size, r, which are preferred for growth.
In order to consider such a system where the growth rate depends strongly on the size-scale, r, the random thermal fluctuations acting on the system need to be decomposed into Fourier components of different wavelengths, and wavenumbers, q = k = 2p/l. A definition of such a Fourier decomposition is that independent Fourier components at wave vector, q, i.e. fq, can be discussed, from a thermodynamic and kinetic perspective, independently. A deviation in concentration, from the mean value, dfq, in a linear approximation, is generated by a chemical potential difference, Yq. This response in a concentration fluctuation, dfq, is described by the response coefficient, aq,
![]()
It can be shown, Strobl pp. 406, that the intensity scattered at q = 4p/l sin(q/2), is proportional to aq,
![]()
The solution to the differential equation of continuity, given above, reflects an exponential growth in concentration with time which is governed by the free energy expression given by the Ginzburg-Landau Functional.
f
(r, t) - <f> = df(r, t) = S exp[t R(q)] {A(q) cos(q dot r) + B(q) sin(q dot r)}Hashimoto equation II-3, where for isotropic scattering q => q.
where R(q) is the linear growth rate for phases at wavenumber "q" associated with wavelength
l, given by,![]()
The term in brackets above reflects the applied potential so the observed scattering will follow an exponential growth in time (at early stages of spinodal decomposition),
S(q) = S(q, t = 0) exp[2 t R(q)]
where R(q) is given above.
d
2g/df2 is a measure of the direction of curvature of the free energy versus composition curve, i.e. in the nucleation and growth regime the curve is concave up so d2g/df2 is positive and in the spinodal regime the curve is concave down and d2g/df2 is negative. For the nucleation and growth regime the growth rate, R(q), is negative (b' is a positive size-related parameter) and no growth occurs spontaneously. For the spinodal regime R(q) can be positive if d2g/df2 > 2b'q2, implying a critical (maximum) q for phase growth (or a minimum size for phase growth since l = 2p/q). This value of q is termed a critical q, qc,qc = (-(
d2g/df2)/2b')1/2The maximum growth occurs for dR(q)/dq = 0, or
d2g/df2 = -4 qmax2 b',qmax = (-(
d2g/df2)/4b')1/2 = qc/├2and
R(qmax) = -DAB (
d2g/df2)/8b'The position of the maximum growth rate and the critical growth rate are governed by thermodynamics and size alone, i.e. there is no transport term, while the rate at the maximum is governed by thermodynamics and transport. The presence of a maximum size of growth reflects a balance between transport and thermodynamics. The expression for R(q) reflects this balance between thermodynamics and kinetics. At small q, q < qmax, or large size, thermodynamics favors rapid decomposition while the rate term's transport prefactor leads to slower growth (q2 dependence of the prefactor). At large q, q > qmax, or small sizes, the thermodynamic term (in brackets) lowers the rate due to the -2
b'q2 term.The expression for qmax and R(qmax) can be used to explain the difficulty of kinetic studies of spinodal decomposition in metals and the relative ease of spinodal studies in polymers. Polymers are large molecules so the term
b' is typically on the order of close to a micron in size, where as for metals it is of atomic dimensions. This means that spinodal decomposition, for thermally similar systems, will be studied with laser light scattering for polymers and x-ray or neutron scattering for metals. Typically, a light scattering pattern can be easily collected in seconds while x-ray or neutron scattering patterns require times on the order of hours. This size difference, coupled with much higher transport coefficients, DAB, for metals leads to decomposition rates on the order of seconds for metals and on the order of minutes for polymers. This means that despite, Cahn-Hillard theory's original development for metals, the only real systems where spinodal decomposition can be studied in-depth, without special quenching procedures etc., are polymeric!Since the terms DAB and (
d2g/df2) are coupled in the Cahn-Hillard approach, these terms are often referred to as the apparent diffusion coefficient, Dapp, reflecting both thermodynamic and transport properties,Dapp = DAB(d2g/df2)
The apparent diffusion coefficient reflects the sharpness of the spinodal peak in small-angle scattering,
![]()
It can be obtained from a plot of R(q)/q2 versus q2, following the equation for R(q) above, Dapp is the intercept at q2 = 0 (in the low-q region where transport dominates).
There is a great deal of self-consistency required by Cahn-Hillard theory in the function R(q). A plot of R(q)/q2 versus q2 yields Dapp as the low-q intercept and 2b' as the slope. These can be used to calculate the growth rate at maximum, the q value at maximum and the critical maximum q at which the growth rate goes to 0. This means that any two features of the spinodal growth rate curve will predict the entire curve! Demonstration of self-consistency in a spinodal curve is therefore evidence that the Cahn-Hillard theory is appropriate for a data set.
In addition to self-consistency within the R(q) curve several other requirements exist for an observation of spinodal decomposition. Since Cahn-Hillard theory relies on thermodynamics, it is usually required that the phase separation observed is reversible on annealing in the single phase region. Also, it is usually required that something resembling a web-like, bicontinuous structure be observed microscopically. Finally, a basic requirement is that the spinodal peak in the scattering curve remain at a single value of qmax during growth. The latter requirement is an indication that no real interfaces are present in the system, since all theories for phase growth in size require an interface term and an associated interfacial energy which is minimized. In Cahn-Hillard theory there is no interface, only a concentration gradient as seen in figure 3.24.
The decay of qmax at "intermediate stages" of spinodal decomposition is an indication of the breakdown of the Cahn-Hillard assumptions. Figure 3 of the Hashimoto paper (Macro 16,644) shows early and intermediate stage spinodal decomposition data from Polystyrene/Polyvinylmethyl ether blends (PS/PVME), demonstrating the behavior of qmax. "Late stage" spinodal decomposition involves the growth of phase size due to minimization of surface area following Oswald Ripening, as will be discussed below. The final phase structure of a spinodal decomposition through Oswald Ripening is indistinguishable from that of a nucleation and growth process.
Application of the Flory-Huggins Equation to Cahn-Hilliard Theory.
The Flory-Huggins equation can be substituted for g(f) in the Ginzburg-Landau Functional. For a simple system of matched molecular weights this results in equation II-15 of Hahsimoto,
![]()
where Dc is the self-diffusion coefficient for translational diffusion which scales as N-2. R0 is the unperturbed coil size, n1/2a. cs is the interaction parameter at the spinodal. From comparison with the general, Cahn-Hillard equation given above,
Since c is proportional to 1/T,
![]()
Plots for a Cahn-Hillard Analysis:
In order to perform a Cahn-Hillard analysis of small-angle light scattering from a spinodally decomposing blend a series of scattering patterns (I versus q) are taken as a function of time (Figure 4 of Hashimoto paper and Figure 3.33 pp. 124 of Strobl). The equation,
S(q) = S(q, t = 0) exp[2 t R(q)]
suggests plots of ln(S(q,t)/S(q,t=0)) versus time, t, to obtain the rate constant R(q). This is done for a series of q values as shown in Hashimoto Figure 5 and Strobl Figure 3.34. In the Strobl figure a negative rate constant is observed for high-q, above qcritical, as expected. (The ln(S(q,t)/S(q,t=0)) versus t curve tails over (Hashimoto Figure 5) as late stage spinodal decomposition is approached, see also Hashimoto Figure 4 where the decay of the peak position at late stage is shown.)
R(q) versus q results obtained from these plots is then plotted as a function of q to obtain the q value at maximum growth rate, qmax, which should correspond to the location of the spinodal peak in the original scattering pattern, Figure 6 of Hashimoto.
In a plot of R(q)/q2 versus q2 for high-q values (beyond the peak in q) the intercept at R(q) => 0 yields the critical q, qc. This value should equal ├2 qmax. This is shown in Figure 7 of Hashimoto.
Oswald Ripening and Deviations from Cahn-Hillard Predictions:
As phase separation progresses, by a spinodal process, the scattering peak is observed to decay in qmax position. This process is usually broken into two regimes, intermediate-stage spinodal decomposition, where modifications of the Cahn-Hilliard approach are appropriate, and late-stage decomposition where a different mechanism based on reduction of surface area is usually used.
In intermediate stage spinodal decomposition, account can be made of a decay in qmax by normalization of the ln(I/I(0)) versus q plot through the x-axis parameter, q/qmax. Such a plot is shown in Strobl Figure 3.36, pp. 127. Hashimoto shows the decay of qmax in Figure 9. In intermediate stage spinodal decomposition, the substitution of q/qmax for q allows direct application of Cahn-Hilliard theory to the data. This approach ignores the importance of the development of interfaces in the decomposition process.
Scattering offers a direct interpretation of the development of interfaces through Porod's Law which describes high-q scattering from a system which displays sharp and smooth interfaces (i.e. oil and water type system). Porod's law states that the scattered intensity, S(q) equals 2p r2SV, where r is a contrast factor such as electron density for x-rays, and SV is the surface to volume ratio for a two phase system. In a log intensity versus log q plot the Porod Regime can be easily identified by marking off 4 decades in I and one decade in q and drawing a line of slope -4. A Porod regime is observed in Figure 3.36 of Strobl, pp. 127. The decay in the prefactor to the power-law decay in time, shown in the lower graph of Figure 3.36, shows that the surface area of the sample is decreasing as a result of Oswald ripening, i.e. phase growth driven by coalescence of small domains into larger domains.
A number of theories have been proposed for late stage coalescence of phases. There remains significant debate over the description of this growth. Since the process is largely decided by kinetics it is doubtful that a clear picture of this process (especially compared to Cahn-Hilliard theory) will result.
Block Copolymers:
One of the most active areas in polymer morphology has been in micro-phase structure of block copolymers. This subject is reviewed in the article by Bates as well as in section 3.3 of Strobl. Block copolymers have, in some sense, achieved the goal of mixed properties for mixtures of polymers which was hoped to be obtained in polymer blends. These combined properties are only achieved at the cost of specialized synthetic schemes using usually anionic, living polymerization (extremely water sensitive). None the less, block copolymers have achieved a degree of commercial success especially in the elastomer industry where the higher cost of these polymers can be offset by their processability, i.e. they can be extruded and injection molded.
Common types of block copolymers are styrene-b-butadiene
(CH2-CH=CH-CH2)x-(CH2-CH(C6H5))y)
and styrene-b-isoprene
(CH2-CH=C(CH3)-CH2)x-(CH2-CH(C6H5))y)
Common topologies:
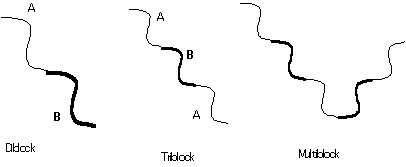
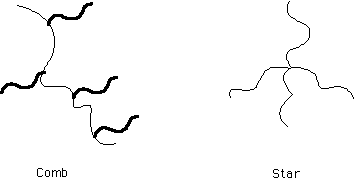
Polymer blends undergo phase separation point the interaction parameter reaches a critical value. In block copolymers a related transition occurs called the disordered to ordered transition. Block copolymers can never reach a completely homogeneous state because of the connectivity of chains, i.e. there will always be large correlations between A and B blocks in a diblock. Similarly, and for the same reason, block copolymers can not achieve macroscopic phase separation. The disorder to order transition is characterized by the formation of microphase separated domains.
One way to look at this transition is in terms of the location of the connecting points between A and B blocks in a diblock copolymer. In the disordered state these connecting points are randomly arranged. After microphase separation these connecting points become ordered. Because of this, the microphase separation point has some similarities to first order transitions such as the melting point. One difference is that the ordered state (crystalline lattice) can be tuned by the block copolymer composition. A second difference is that there is no change in density on microphase separation.
The connection of diblock copolymer segments enhances miscibility over an analogous blend. The critical interaction parameter for a symmetric 50:50 blend is 2/N. For a similar block copolymer system (50:50 fractions) the critical interaction parameter is about 10.4/N. Variants of the RPA equation are needed to determine the interaction parameter for these systems.
The two most important characterization techniques for block copolymers are TEM and small-angle x-ray scattering because structural transitions occur on the colloidal scale. The microphase separated state in a diblock systems is characterized by a series of peaks. The lattice type can be determined by the sequence of these peaks in q. The first peak (brightest) can be used to normalize q, then the orders of peaks follow the sequence,
Lamellar (other than exactly 50:50)
1; 2; 3; 4;....
Lamellar (exactly 50:50)
1; 3; 5;...
Hexagonal Rods (2-d arrangement)
1; 1.72; 2; 2.63; 3;...
Cubic Spheres (3-d arrangement)
SC: 1; 1.48; 1.72; 2; 2.22; 2.44; 2.86; 3.0; ...
BCC: 1; 1.48; 1.72; 2; 2.22; 2.44; 2.63; 2.86; ...
OBDD: 1; 1.22; 1.48; 1.72; 2.0; ...
RPA and Block Copolymers/Density Fluctuations:
Concentration Fluctuations in Polymer Solutions:
(Follows Gert Strobl "The Physics of Polymers 2'nd Ed. 1997 Appendix A4 but follows Doi section 2.2 fairly closely)
A polymer in dilute solution is a single phase but contains concentration fluctuations related to chain connectivity and random thermal motion. The Flory-Huggins approach ignores these concentration fluctuations so is not applicable near the critical point where fluctuations are high and is really not appropriate for discussions of small-scale features except in an average sense. The Flory-Huggins statistical model uses an average interaction energy which is termed a "mean field" approach. As concentration is increased in a polymer solution, screening leads to a reduction in the effect of connectivity based monomer density fluctuations. In a pure melt all connectivity based segmental fluctuations, of this kind, are screened leading to Gaussian scaling.
Much of modern polymer theory is based on an understanding and description of concentration fluctuations. This is because a description of such fluctuations are a natural way to describe random systems with statistical features. Fluctuations in density can be described in terms of a series of wavelengths, that is, any distribution of density in space can be decomposed into a series of sin waves of different magnitude. For each wavelength there is an associated wave number, k = 2p/l, associated with that type of fluctuation. The amplitude of a density fluctuation at wave number k (and wavelength l) which contributes to the density profile of a sample in space, r, can be denoted fk.
1) Fluctuations of wavenumber "k" can be considered independently of other wavenumber fluctuations.
2) Incompressibility is an assumption of almost all theoretical approaches so fk refers to one component of a mixture but the other component is just - fk, so fluctuations of component A are matched by opposing fluctuations of B in the opposite direction to yield an average concentration for each wavenumber.
Density fluctuations of fk follow Boltzman statistics so the probability of a fluctuation of size fk is given by,
p(fk) ┼ exp(-ak fk2/2kT)
where ak is the inverse of the response of the density, fk, to a potential field, Yk,
f
k = Yk/ak = ak Yk(The increase in free energy, dG associated with a concentration fluctuation, fk, is given by,
d
G = ak fk2/2 = Yk dfk)The mean square value, < fk2> = kT/ ak = kT ak
The scattering function per lattice site of volume Vc, Sc(q=k) is related to this mean square fluctuation by,
Sc(q) = kT ak/Vc
The calculation of a scattering function, Sc(q=k), is the equivalent of calculation of response functions, ak.
Random Phase Approximation (RPA):
One of the major accomplishments of the density fluctuation approach described above was the calculation of the scattering function for a polymer/polymer mixture and for block copolymers in the single phase state. These scattering functions are composed of Debye scattering functions which describe the coils in a dilute solution at the theta temperature. Prior to the development of the random phase approximation (early 1980's) it was not possible to directly determine the interaction parameter for polymer blends from scattering data. This is now the primary method of determination of the interaction parameter. Additionally, application of the RPA approach to block copolymers is the primary method of determination of the thermodynamics of these systems. If one were to combine all polymer physics papers from the last 5 years more than half would involve in some way use of the RPA approach. Despite the fact that this approach is exclusively used with scattering analysis, it is of pivotal importance to have some understanding of it in order to understand recent literature as a whole.
The RPA approach is an extension of the composition fluctuation ideas presented above. Consider an athermal mixture of two polymer chains, A and B. Consider that the B chains have 0 contrast so are not observable. If a potential, Yk, is applied to this system that only acts on "A" chains and which leads to excitation of a concentration fluctuation of wave vector "k", fk, we can write,
f
k = ak0 Ykwhere ak0 is the collective response coefficient for lattice units of chain "A" under athermal conditions (hence the superscript 0) in a mixture with chains "B". Under the discussion above, ak0, is associated with the scattering from the mixture of "A" and "B" chains.
A fluctuation of concentration in "A" leads to a negative fluctuation of "B" due to incompressibility.
f
k = fkA = -fkBThis response of "B" units to a fluctuation in "A" units reflects the internal induction of the system. "B" units respond as if they were subjected to a potential Yk even though "B" units do not respond to the external field which is applied. Yk is called the "internal field".
A-chains respond to both the internal field, Yk, as well as to the external field Yk.
f
k = akAA (Yk + Yk)where akAA is the single-chain response coefficient of "A" units response to forces acting on other "A" units. This is different than ak0 which reflects the response of an "A" unit to an external field. For chains in a melt it is assumed that the Gaussian state is displayed due to screening so analytic forms based on the Debye scattering function apply to describe the single-chain response coefficients. That is, we already have an analytic form which describes scattering associated with akAA.
"B" units respond only to the internal field, Yk, since the external field, Yk, acts only on "A" units as introduced. Thus,
f
kB = -fk = akBB (Yk)The collective response coefficient, ak0, is associated with the scattering from the mixture of "A" and "B" chains. In order to determine ak0 from the known Debye functions for akAA and akBB, the induced field, Yk, must be expressed as a function of the known functions and the applied field, Yk,
Y
k = Yk akAA/( akAA + akBB)Through addition of the two expressions above. This expression can then be used in the expression for fk above to yield,
f
k = Yk { akBB akAA/( akAA + akBB)}and by comparison with the first expression of this section yields,
1/ ak0 = 1/ akAA + 1/ akBB
The latter implies that the inverse of the scattering function for a polymer blend is an inverse sum of the scattering functions for the two components.
For non-athermal systems, an external potential Yk leads to a concentration wave fk which produces a molecular field, c' fk, where c' = 2ckT/Vc. If c' is positive the field is enhanced and if c' is negative the external field is diminished.
f
k = ak0 (Yk + c' fk)This can be solved for fk to yield,
f
k = ak0 Yk/(1 - c' ak0)The non-athermal collective response coefficient, ak, is associated with the scattering from a non-athermal polymer blend. This response coefficient can be directly obtained from the above expression by comparison with the definition of the collective response coefficient,
a
k = fk/ Yk = ak0/(1 - c' ak0)or
1/ ak = 1/ ak0 - c'
Using the previous expression for 1/ ak0 we have,
1/ ak = 1/ akAA + 1/ akBB - 2ckT/Vc
(For a polymer solution akBB is a constant in k.)
Block Copolymers and the Random Phase Approximation:
For an athermal system composed of a block copolymer of A and B segments, the description of concentration fluctuations parallels that for a polymer blends except that response coefficients related to the connectivity of A and B chains must be included. akAB reflects the reaction of A units to a force acting on B units in the same chain (at wave vector k). A response coefficient akBA reflects the reaction of B units to a force acting on A chains (at wave vector k). In parallel with the athermal blend derivation above,
f
k = akAA (Yk + Yk) + akAB Ykand
f
kB = -fk = akBB (Yk) + akBA (Yk + Yk)The last term representing a force acting on an A unit and the response of a B unit so includes the internal and external fields. The internal field, Yk, can be removed by summation of the two equations under the assumption of incompressibility, fkB = -fk,
Y
k(akAA+ akAB + akBB + akBA) = -Yk (akBA + akAA)Y
k = -Yk (akAA + akBA)/(akAA+ akAB + akBB + akBA)This can be substituted in the expression for fk yielding,
f
k = Yk {akAA - [akAA + akAB] (akAA + akBA)/(akAA+ akAB + akBB + akBA)}and,
a
k0 = fk/Yk={akAA - [akAA + akAB] [akAA + akBA]/(akAA+ akAB + akBB + akBA)}= (akAA akAA + akAA akAB + akAA akBB + akAA akBA - akAA akAA - akAAakBA - akABakAA- akABakBA)
(akAA+ akAB + akBB + akBA)
ak0 = (akAA akBB - akABakBA)/(akAA+ akAB + akBB + akBA)
The latter representing the RPA for athermal block copolymers. The thermal system can be calculated using the same approach as for thermal blends given above,
1/ ak = 1/ ak0 - c' = (akAA+ akAB + akBB + akBA)/(akAA akBB - akABakBA) - 2kTc/Vc
To obtain the scattering functions we substitute,
a
k=qAA = Vc fNASD(RAq)/kTand
a
k=qBB = Vc (1 - f) NBSD(RBq) /kTwhere Ni is the degree of polymerization for chains of type "i",
f,is the dilution of chains A in the block copolymer, SD is the Debye scattering function for a polymer coil and Ri is the coil's Gaussian radius of gyration. The Debye function is the Fourier-transform of the pair distribution function g(r) for the pairs of type AA or BB.To calculate
akAB we need the pair distribution functions for the probability of finding a B or A monomer at a distance r from each other. The latter can be analytically solved as a function of the single chain structures. One result of this is that akAB = akBA. The functional form is,a
k=qAB = Vc (NABSD(R0q) - fNASD(RAq) - (1 - f) NBSD(RBq))/(2kT)where NAB = NA + NB, and R02 = RA2 + RB2.
Block copolymers display a "natural" correlation distance which is a result of segregation of A and B blocks in a single phase melt. This "natural" distance of segregation is reflected in the athermal equation for instance.
a
k0 = (akAA akBB - akABakBA)/(akAA+ akAB + akBB + akBA)Consider the summation of response coefficients as a summation of Debye functions. For a 50/50 block copolymer NA = NB, and RA ┼ RB, then R0 is ├2RA, i.e. R0 is bigger than RA. It can be easily verified that the subtraction of two Debye functions of differing R yields a curve with a correlation peak (see figure below). Thus, even in the single phase melt, block copolymers display a correlation peak.
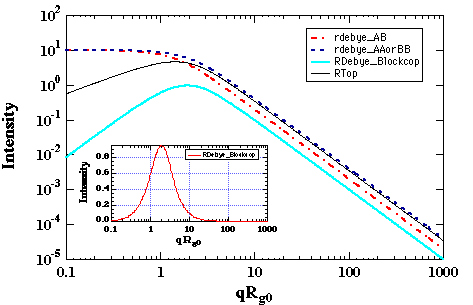
Variation of c' in the thermal system leads to the determination of a critical point where the intensity becomes infinite as shown below:
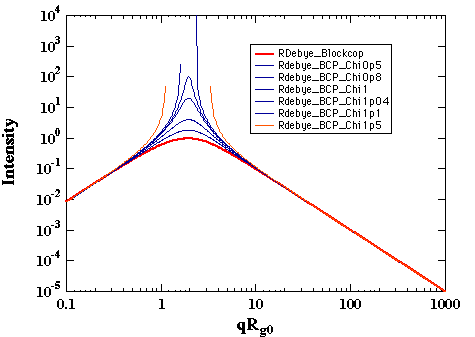
For symmetric diblock copolymers ccNAB = 10.4. This is the lowest value for ccritical, i.e. other compositions will have higher values. This value should be compared with the critical c for the same two polymers in a symmetric binary blend, ccN = 2. The higher value for the critical point in a block copolymer reflects the connectivity of the polymer chains which suppresses phase separation to a higher value of c (lower temperature).
When phase separation occurs in a block copolymer the domain size is restricted by the connection of the A and B chains. This leads to a variety of micro-phase separated structures. When one chain is much shorter than the other, NA<<NB, spherical domains form. For more closely matched molecular weights rods of the minor phase form. When NA ┼ NB, the system forms lamellar domains. The size of these domains is governed by thermodynamics as discussed below.
Domain Size in Phase Separated Block Copolymers:
The size and separation distance of lamellar domains (for example) can be predicted using thermodynamics. The change in Gibbs free energy, DG, for the transition from a homogeneous system to the micro-phase separated system is composed of an enthalpic term, DH, which has contributions from bulk, DHbulk, and interface, DHint, a change in entropy associated with A-B junction points becoming located at the interface, DSint, and a change in entropy associated with stretching the chains, DSstr. The bulk enthalpy change is given by Flory Huggins theory as,
D
Hbulk = - kTcNABfA(1-fA)The interfacial enthalpy is associated with an interfacial area, A, a transition layer thickness dt,
D
Hint = + kT c A dt/VcThe loss in entropy by location of A-B junctions at the interface is given by,
D
Sint = k ln(dt/(dA + dB)) = k ln(dt/dAB)where dA is the thickness of the A layer and dB is the thickness of the B layer and dAB is the repeat period for the lamellae. The loss in entropy due to stretching of the chains is given by,
D
Sstr = -kb2(dAB/R0)2Also, the volume of a chain is given by Vc NAB = A dAB
D
G = DHbulk + DHint - T DSint - T DSstrbecomes,
D
G/kT = - cNABfA(1-fA) + c A dt/Vc + ln(dt/dAB) + b2(dAB/R0)2Setting the derivative with respect to "A" to 0, neglecting the "ln" term which does not have a significant derivative (using dAB = Vc NAB / A in the last term),
(1/kT) dDG/dA = c dt/Vc - 2b2(Vc NAB /R0)2/A3 = 0
yields,
A ┼ Vc (2 NAB2 /( c dt R02))1/3
using R02 = Vc2/3 NAB
A3 ┼ Vc7/3 NAB/(c dt)
and
dAB = NAB2/3 Vc2/9 (c dt)1/3
This molecular weight dependence has been observed experimentally.
=>Back To Characterization Lab
Download this page: =>Phase Behavior.pdf