Chapter 5

=> Return to Physics.html

G. R. Strobl, Chapter 6 "The Physics of Polymers, 2'nd Ed." Springer, NY, (1997).

R. B. Bird, R. C. Armstrong, O. Hassager, "Dynamics of Polymeric Liquids", Vol. 2, John Wiley and Sons (1977).

M. Doi, "Introduction to Polymer Physics", Oxford Science Publishers (1996).

M. Doi, S. F. Edwards, "The Theory of Polymer Dynamics", Clarendon Press (1986).

de Gennes,"Scaling Concepts in Polymer Physics" (1979).

K. S. Schmitz,"An Introduction to Dynamic Light Scattering by Macromolecules" Academic Press, 1990

P. Heimenz, "Polymer Chemistry"

Chapter 5: Molecular Scale Models for Macroscopic Dynamic Response
Fluctuation-Dissipation Theorem:

Molecular scale models (microscopic models) can be used to quantitatively predict material properties in the context of linear response theory presented above. A basic premise or theorem of statistical thermodynamics on which such predictions are based is the Fluctuation Dissipation Theorem. This theorem is based on weak fields relative to the potential of molecular interaction so that rates of relaxation are not effected by the applied field. The Fluctuation-Dissipation Theorem proposes that there is an explicit relationship between molecular dynamics at thermal equilibrium and the macroscopic response that is observed in a dynamic measurement. A description of the Fluctuation-Dissipation Theorem, then, is a prerequisite for the development of molecular scale models for polymer dynamics.

Thermodynamics deals with a volume of material where molecular scale features occur in vast numbers, so that statistics can be used to describe the thermal properties. Consider such a volume element, v, that is small enough that fluctuations in temperature and density, for example, can be observed but large enough to be described as a thermodynamic volume element. Random, thermal and density fluctuations occur due to the motion of molecules at a finite temperature. These fluctuations lead to fluctuations in stress and dipole moment (for a molecularly polar system). The superposition of the molecular scale dipole moments, p_i, result in a net dipole moment due to thermal fluctuations in this small volume element,

p_v(t) = ·p_i(t)

The dipole moment for such a volume element varies with time. The average value over a long period of time, relative to the rate of fluctuation, is 0. We are interested in the time required for a thermal fluctuation to randomize, i.e. for the average to become zero. This can be determined from the shape of the second order time correlation function that relates the polarization at a time time = t₀ to the polarization at a time time = t, averaged over all times t₀, <p_v(t₀)^.p_v(t)>. If we consider only one direction in 3-d space then <p_v(t₀)^.p_v(t)>_x = <p_v(t₀)^.p_v(t)>/3.

Consider the response of same material to an applied electric field, E₀, that produces a polarization P, P = e₀De(t)E₀. At equilibrium the polarization, P, is given by P = e₀De(°)E₀. If, after reaching equilibrium the field E₀ is turned off, then the bulk polarization will decay according to P = e₀ E₀ (De(°) -De(t)).

The fluctuation dissipation theorem proposes a relationship between the response of the volume element to random thermal fluctuations in one direction, <p_v(t₀)^.p_v(t)>_x, and the decay observed in the bulk material in response to an external field, E₀,

<p_v(t₀)^.p_v(t)>_x = vkT e₀ (De(°) -De(t))

The left side is directly related to molecular dynamics through the first equation. The second term is directly related to bulk behavior through the description of dielectric relaxation. Then the fluctuation-dissipation theorem gives justification to the calculation of macroscopic/bulk dynamic properties from theories and models for equilibrium fluctuations.

A parallel equation can be proposed for stress relaxation,

<s_v(t₀)^.s_v(t)>_x = kT G(t)/v

Stress is an intensive variable, i.e. it is a volumetric average (divided by v), while the total dipole moment is an extensive variable (proportional to v).

The limit of the time correlation function at t = t₀ gives the variance for the polarization or for the stress induced by thermal fluctuations,

<p_v²>_x = vkT e₀ De(°) and <s_v²>_x = kT G(0)/v

In both cases the variance for thermal fluctuations increase linearly with the temperature.

Generic Description of the Fluctuation-Dissipation Theorem:

For a generic extensive variable X_v(t) that is a linear response to a field, y, we have,

X_v(t) = v a(t) y₀ (t>=0)

where a(t) is the time dependent susceptibility. The time correlation function for the generic extensive variable is given by,

<X_v(t₀)^.X_v(t)> = vkT (a(°) - a(t))

(ignoring flow to ensure a t => ° limit).

For a dynamic response, X_v(w), the spectrum of the response in frequency; or the spectral density, <X_v²(w)>, is related to the time correlation function by a Fourier transform,

and the inverse of this Fourier transform defines the time dependent response in terms of the spectral density,

The spectral density, <X_v²(w)>, can be though of as how power (a real number so the square of the imaginary response) is distributed in a responding system after a perturbation.

We desire an expression for the fluctuation-dissipation theorem in terms of the spectral density of the response, <X_v²(w)>, or the spectral density of the applied field, <y²(w)>. To obtain this expression we need to use the limiting identity that the time dependent susceptibility at infinite time, a(t=>°) equals the real part of the dynamic susceptibility at zero frequency, a'(w=>0). We have, above, <X_v(t₀)^.X_v(t)> = vkT (a(°) - a(t)), and using the Fourier expression for the time correlation function (at t = 0),

The Kramers-Kronig dispersion relation (previously discussed) defines a'(w=>0) as,

This can be used to relate the arguments of the two integrants (agruments of the integrals),

This defines the spectral density, <X_v²(w)>, as,

<X_v²(w)> = 2vkT a"(w) / w

This is a second form for the fluctuation-dissipation theorem that relates energy dissipation, a"(w), as previously demonstrated, to the spectral density of the fluctuations.

A similar development can be made for a dynamic creep measurement relating the spectral density of the field fluctuations to the dissipation as described by the imaginary part of the general dynamic modulus, a"(w),

<y²(w)> = 2kT a"(w) / (vw)

where the subscript v is absent for y since it is an intrinsic parameter. The dynamic modulus, a*, is related to the dynamic susceptibility, a*, by a* = 1/a*.

The Fluctuation-Dissipation Theorem and the Glass Transition (Perfect Together?):

The measurement of the dynamic response of a linear system (for small magnitude perturbations) are identified with a spectral analysis of equilibrium fluctuations due to thermal motion by the fludtuation-dissipation theorem. A system such as a polymer displays many dynamic modes. Consider a guitar string of length L. Vibration of the string can occur with one large sine wave of wavelength 2L, a smaller wave of wavelength L and many other modes of length 2/3 L, 1/2 L and so forth. A polymer chain is analogous but more complex including both normal modes in the chain direction as well as modes associated with the a-process at the glass transition and lower temperature b, and g-modes and so on. We have shown that the response in dielectric and mechanical compliance and modulus measurements can probe these modes of response. For the a-process modes at the glass transition, we have shown that the average relaxation time by these different techniques shows similar scaling behavior in temperature but different values (Strobl figure 5.18).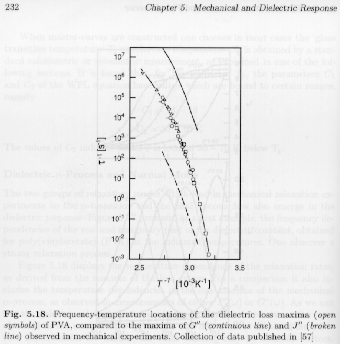

Since it appears that all of these techniques are related to the a-modes of relaxation near the glass transition it seems that the different measurements weight these various modes in different ways leading to identical scaling for the weighted average but different values. For a-mode responses, changes in the dipole moment lead to the dielectric response, changes in the shape of the polymer lead to the compliance response and changes in the stress distribution lead to the modulus response. The relaxation times for the a-modes span 4 orders of magnitude, so the different weighting schemes can have dramatic impacts on the average value for relaxation time. From figure 5.18 it can be seen that compliance (change in shape of the polymer) weights the longest relaxation times higher, while modulus (changes in the stress distribution) weights the shortest relaxation times higher. Dielectric resoponse (changes in the dipole moment) apparently weight the intermediate relaxation times higher.

The Fluctuation-Dissipation Theorem as a Basis for Molecular Models:

The reason to discuss the fluctuation dissipation theorem in the context of this class is that it is the fundamental justification for the development of molecular scale models of polymer dynamics as indicators of bulk dynamic response. The fluctuation dissipation theorem tells us that we need to develop models on the molecular scale that predict the equilibrium time correlation functions for responses. The fluctuation dissipation theorem then relates these correlation functions to the response functions.

Several models for molecular scale dynamic response have formed the core of our understanding of polymer dynamics. The first model, "Rouse-model" is appropriate for the description of oligomeric chains below the entanglement molecular weight or polymers in solution below the overlap concentration, i.e. dilute solutions. The second model, "reptation-model" can describe some of the properties above the entanglement molecular weight, polymer melts and concentrated solutions. The final model deals specifically with polymer chains in solution from a hydrodynamic sense, the "hydrodynamic model". With these tools we will have a fundamental basis for understanding polymer dyanmics.

=> Return to Physics.html