G. R. Strobl, Chapter 6 "The Physics of Polymers, 2'nd Ed." Springer, NY, (1997).
R. B. Bird, R. C. Armstrong, O. Hassager, "Dynamics of Polymeric Liquids", Vol. 2, John Wiley and Sons (1977).
M. Doi, "Introduction to Polymer Physics", Oxford Science Publishers (1996).
M. Doi, S. F. Edwards, "The Theory of Polymer Dynamics", Clarendon Press (1986).
de Gennes,"Scaling Concepts in Polymer Physics" (1979).
K. S. Schmitz,"An Introduction to Dynamic Light Scattering by Macromolecules" Academic Press, 1990
P. Heimenz, "Polymer Chemistry"
Chapter 6: The Rouse Model
The Bead (friction factor) and Spring (Gaussian entropy) Molecular Model:
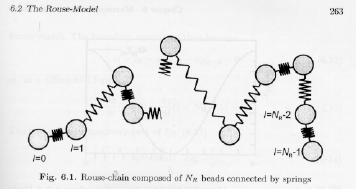
The Rouse model is based on dividing the polymer chain into subsections that are sufficiently large to display rubber like elasticity (springy behavior as small elongations). The subsections of the chain, in the Rouse model, have a roughly spherical shape (bead shape) and present a mechanical drag with respect to the remainder of the melt or solution that can be quantified with a single term, the subsections friction factor for small motions. The two elements of a single subsection can be represented in series as a spring of no volume and a rigid bead of infinite modulus. This model for a chain is shown in Strobl's figure 6.1 below.

The Spring:
The Rouse model is based on a Gaussian (
q-condition or relaxed melt conformation) for the coil subsection. Under this assumption rubber elasticity theory can be used to estimate the spring constant for the subsection based on the number of mer units in a subsection or the mean square of the end-to-end distance for a subsection, <Dr2>. For a subsection with end points at Dr the tensile force associated with this end-to end distance, f, is given by fel = b Dr, where b is a force constant or spring constant for the Rouse subsection of the chain. b is given by rubber elasticity for small deformations and Gaussian conformations as, b = 3kT/<Dr2>. b decreases with chain size since <Dr2> = nl2 for a Gaussian chain, and increases linearly with absolute temperature as is characteristic of an ideal, entropically derived force, e.g. the ideal gas law PV = nRT.For a colloidal scale particle suspended in a solvent the viscous force associated with drag on the particle is proportional to the velocity of the colloidal particle, fvis = zu where u is the velocity of the particle. The friction coefficient, z, is proportional to the solvent viscosity, hs. In a polymer melt the solvent viscosity parallels the melt viscosity although the friction coefficient will be used first as a generic parameter with no specific definition except that it is constant for a given set of conditions.
The polymer chain is first divided into NR Rouse subsections of arbitrary length much larger than a mer unit but much smaller than the entire chain. Each subsection is represented by a colloidal bead with a friction coefficient zR, and a spring with a spring constant bR. The beads are indexed from 0 to NR -1. In Strobl's figure 6.1, reproduced above, the motion of a single bead leads to opposing tension and compression on the neighboring springs. If the "solvent" moves relative to the bead at a relative velocity of drl/dt, where the subscript "l" refers to the Rouse bead's subsectional index, then restoring forces due to the spring constants on the springs between beads "l+1" and "l" and beads "l-1" and "l" serve to counter act the drag force due to relative motion of bead "l". The balance of the drag force and the elastic forces is given by,
z
R drl/dt = bR (rl+1 - rl) + bR (rl-1> - rl)= bR (rl+1 + rl-1 - 2 rl)
where bR is defined in terms of the number of mer units in a Rouse subsection or the mean squared end-to-end distance for a Rouse subsection, aR2 = Nl2/NR, bR = 3kT/aR2. This assumes that the chains are Gaussian both in the unperturbed state as well as in the perturbed state (a condition that is not likely to be fulfilled).
We consider thermal motion for the Rouse subsectional beads so that motion in x, y, and z directions are equivalent and can be treated independently. Strobl considers the z-direction, and replaces the vector r with the scalar z for simplicity. The balance of forces above becomes then,
z
R dzl/dt = bR (zl+1 + zl-1 - 2zl)For a chain of infinite molecular weight the beads are, on average, indistinguishable. For this case we can propose a wave behavior for the average bead position, zl,
zl = k exp(-t/t) exp(i l d)
that includes an exponential time decay or damping and a phase shift, d, between adjacent beads. This solution can be proposed since, for an infinite chain with no inertial effects, the beads are all equivalent (Strobl's translational symmetry). Use of the wave solution in the 1-d equation results in,
-z
R k/t exp(-t/t) exp(i l d) = k bR exp(-t/t) (exp(i (l-1) d) + exp(i (l+1) d) - 2 exp(i l d))-z
R/t exp(i l d) = exp(i l d) bR {exp(-id)+exp(id) - 2}-z
R/t = 2bR {cos(d) -1}Using exp(-i
d) = cosd - i sind and exp(+id) = cosd + i sind. Also, 2 sin2 A = (1 - cos 2A), so,t
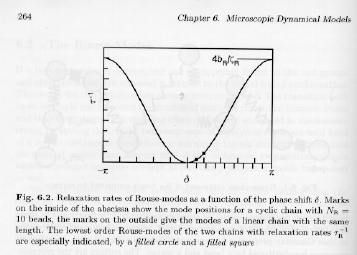
= zR/{4bR sin2(d/2)}This is shown in Strobl's figure 6.2. For an infinite chain the relaxation time is a continuous function of the phase angle, d. That is, there are no discrete modes but a continuous relaxation function.
Rouse for a Finite Chain:
The analysis based on a wave function describing position is true for an infinite chain where there is no distinguishing feature between different average Rouse units. The simplest way to deal with finite length chains is to assume that the chain is a loop so the assumption of indistinguishable units can be maintained. Assuming the chain is a loop leads to zl
= zl+N, where N is the number of Rouse units in the chain. For this case there are discrete modes associated with the wave solution, the modes being defined by Ndm = 2p m, where m is an integer defining which mode of vibration is considered. There are N modes of vibration for a cyclic solution to the Rouse differential equations:d
m = 2p m/N, with m = (N/2 -1) to N/2 for cyclic boundary conditionsCyclic boundary conditions lead to a discrete number of modes but are not totally appropriate for most real polymers. For a real chain under the Rouse assumption that the Rouse bead is only sensitive to neighboring bead positions, the two end-groups for a linear chain become distinguishable. Tensile forces vanish for these two end-groups, bead 0 and bead N - 1 for a chain of N beads with the index begining at 0. Since for bead 0 and bead N - 1 there are no tensile forces and no velocity relative to the chain, we have,
dz/dl (l = 0) = dz/dl (l = {N-1}) = 0
and,
z
R dzl/dt = bR (zl+1 + zl-1 - 2zl)becomes,
0 = z1 - z0 = zN-1 - zN-2
The wave solution, zl = exp(-t/t) exp(ild) = exp(-t/t) cos(ld) + i exp(-t/t) sin(ld), must be broken into the real and imaginary components since there is no imaginary part at l = 0 and at l = N - 1, i.e. at the two ends of the chain. For the end of the chain, l = N-1, the derivative of the cos term yields,
dz/dl (l = {N-1}) = k sin{(N-1)d} = 0 (from above)
The latter equality can only be met when the argument of the sin term follows,
(N -1) dm = mp
Then, for a linear chain with free ends the following eigenvalues (the differential equations are solved by matrix math usually, see Aklonis/McKnight "Introduction to Polymer Viscoelasticity" for a nice treatment), or Rouse modes can exist,
d
m = pm/(N-1), where m is an integer from 0 to N-1.There are N Rouse-Modes for a linear chain. The difference between this solution and that for the cyclic chain is observed only for short numbers of Rouse units, Strobl's figure 6.2 shows this for a chain of 10 units.
Rouse Modes:
The Rouse model introduces the idea that normal mode relaxations in a polymer chain can be described by a series of sin wave oscillations. These oscillations are describe in terms of the order, m. The 0'th order (m = 0) oscillation corresponds with free translation of the chain where
d = 0, and 1/t = 0. The lowest order mode of interest is for m=1 where,t
1-1 = tR-1 = (4bR/zR) sin2(p/(N-1)))For small A, sin A => A in radians and because N is usually a large number we have,
t
R-1 = (4bR/zR) (p2/(N-1)2) Å 3kTp2/(zR aR2 (N-1)2)aR is the RMS end-to-end distance for a Rouse segment (i.e. a bean and spring) and N is the number of Rouse segments in a chain. It is preferred to describe the Rouse time, tR, in terms of parameters that do not depend on the arbitrary size and number of Rouse segments and this can be accomplished through the identity, R02 = aR2 (N -1), then,
t
R-1 = 3kTp2/(zR R02 (N-1)) = 3kTp2/((zR/aR2) R04)The only term remaining that is associated with the Rouse segment is (zR/aR2). If this is constant then the friction factor for a Rouse segment must be proportional to the number of chain units in a Rouse segment. The latter assumption is sometimes called the free-draining limit. The free-draining limit is a basic assumption of the Rouse model, the friction factor for a Rouse segment is just proportional to the sum of the contributions of individual segments.
The Free draining limit fails, for example, when dilute solutions of polymer coils trap solvent molecules within the individual coils.
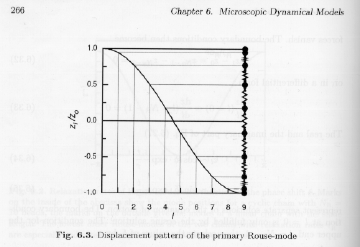
Strobl's figure 6.3 shows the response of the lowest order Rouse Mode, m=1, corresponding to tR, for displacement of one end of a chain relative to the chain.
The expression for the lowest order Rouse mode's relaxation time can be used to describe the molecular weight dependence of the relaxation time since R02 = a02 N0
t
R = ((zR/aR2) R04)/(3kTp2) = ((zR/aR2) N02)/(3kTp2)This is the predicted scaling of the mean viscoelastic relaxation time for non-entangled chains discussed previously, i.e. below the entanglement molecular weight for a polymer melt.
While the longest relaxation time, tR, depends on the molecular weight but not on the choice of the Rouse segment due to the assumption that the friction factor is linear in molecular weight of the Rouse segment, the shortest relaxation time for the Rouse model, m = N -1, depends directly on the choice of Rouse segment size,
t
N-1 = zR/{4bR sin2[p m/((N-1)2)]} = zR/{4bR sin2[p /2]} = zR/{4bR} = aR2 zR/{12 kT}= aR4 (zR/aR2)/{12 kT}
The shortest time is limited by the assumption that the chain is Gaussian within the Rouse segment. Another consideration is that for small segments localized, short time relaxations (a-mode relaxations) gradually begin to dominate the dynamics at small sizes. There is an inherent relationship between small sizes and short times.
Average Properties of a 3-Dimensional Rouse Chain:
The relaxation of the chain is symmetric and independent for the three directions of 3-d space. There are, then, 3N independent Rouse modes for a chain of N Rouse segments. The relative amplitude of response of the m'th mode of a Rouse chain is described by the normal coordinate, Zm,
zl = Zm cos(ldm)
where l is the index of the Rouse bead and m is the mode of vibration.
To determine the average amplitude of a Rouse mode, the free energy of the chain needs to be calculated as a function of the mode of thermal vibration (i.e. vibrations due to thermal fluctuations). The free energy, Dfp, is defined by the summation of rubber elasticity laws applied to each Rouse segment, (summed form l = 0 to l = N-2)
D
fp = (bR/2) S(zl+1 - zl)2 = (Zm2 bR/2) S(cos((l + 1)dm) - cos(ldm))2The cosine difference, for a large chain can be replaced by a derivative with respect to l, leading to,
D
fp = {(dmZm)2 bR/2} Ssin2(ldm)The average of the square of the sine function is 1/2 and the summation over (N-1) terms leads to (N-1)/2 for the summation so,
D
fp(Zm) = (dmZm)2 {bR/2} (N-1)/2
The free energy associated with the Rouse Mode "m" is proportional to the square of the amplitude of the mode's vibrations, Zm
2. This free energy can be used in the Boltzman function to give a probability distribution function for the Rouse mode amplitude, Zm,p(Zm) Å exp(-Dfp(Zm)/(kT))
Since the free energy is proportional to the square of the amplitude this distribution is a Gaussian function. The average value of the free energy, <Dfp>, is proportional to the variance of the amplitude, <Zm2>. For a thermal fluctuation the average free energy is proportional to kT/2 so,
kT/2 = <Dfp> = <Zm2> dm2 {bR/2} (N-1)/2 = <Zm2> dm2 {3kT/(2aR2)} (N-1)/2
by rearrangement,
<Zm
2> = 2 aR2 /{3 (N-1) dm2} = 2 R02 / {3p2 m2}So the variance of the amplitude of the Rouse vibration for mode "m" is independent of the temperature. The largest amplitudes of vibration are for the lowest orders (largest sizes), so that the second order mode has 4 times less amplitude than the first order mode.
The above equation for the amplitude of the Rouse "m"-mode suggests a contribution from a given mode to the mean squared end-to-end distance of the chain, R02 = <R2>. Since the phase angle between Rouse units is given by, dm = pm/NR-1, even numbered modes, m = 0, 2, 4, ... contribute symmetric motions to the overall chain that give a mean square displacement of 0. So only the odd numbered modes, m = 1, 3, 5, 7, ... are considered in calculation of the net contribution of Rouse-modes to the total mean squared end-to-end distance <R2> = R02. Considering only the z-direction, <Rz2> = R02/3 = <(zN-1 -z0)2>, we have,
<(zN-1 -z0)2> = <(2 Z1)2> + <(2 Z3)2> + ... = R02{8/(3 p2)} {1 + 1/9 + ...}
so about 90% of the total end-to-end distance, <Rz2> = R02/3, is related to the lowest order Rouse modes (1 and 3). If only the first order Rouse mode is used, then the entire polymer coil is represented as a single spring between two dumbells!
Dissipation of Fluctuations in the Rouse Model:
Strobl's figure 6.4 shows the expected behavior of a single Rouse mode, "m", in response to random thermal fluctuations.
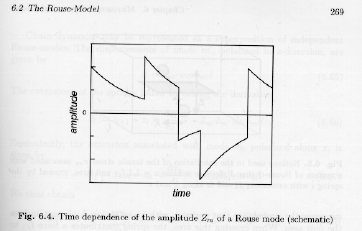
The curve is characterized by sharp displacements due to thermal excitation followed by Rouse relaxation following an exponential decay in time. The time decay is expected to be governed by a single relaxation time for a single mode, tm. The time correlation function for the amplitude of the mode "m" fluctuations, Zm, can be expressed as an exponential depending on this relaxation time,
<Zm(0) Zm(t)> = <Zm2> exp(-t/tm) = [2 R02 / {3p2 m2}] exp(-t/tm)
where tm = zR/{4bR sin2(dm/2)} and dm = pm/(N-1).
For a stress relaxation experiment the fluctuation dissipation theorem relates the time correlation function for the stress with the stress relaxation modulus,G(t),
<szx(0) szx(t)> = kT G(t)/v
The Rouse model can be applied to this equation if the time dependence of the thermal stress fluctuations can be calculated from the Rouse model. A subsystem is defined of volume "v" described by a Cartesian coordinate system of lx, ly, lz, as shown in Strobl's figure 6.5. For a Rouse spring of index "i" the extension is defined in the three Cartesian directions as xi, yi, zi.
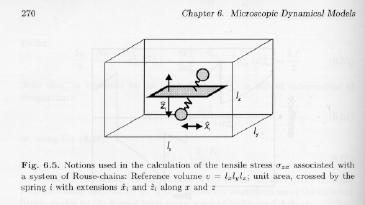
Consider the force, fx, that contributes to the average shear stress, szx, from a Rouse spring element, i, fxi. The shear stress, szx, is calculated by a summation of forces fxi in the x-direction, that act on the x-y plane, the shear stress being this sum of forces divided by the area of the x-y plane under consideration. A given Rouse spring element contributes to this shear stress if it crosses the x-y plane being considered. szx = S fxi, zi/(lx ly lz) = S fxi, zi//vwhere zi is the component of the vector along the spring "i" pointing in the z-direction, and lx, ly and lz are the orthogonal edges of the volume element "v" that is considered in calculation of the local shear stress due to Rouse elements. zi/lz gives the probability that spring "i" crosses the lx-ly plane within the volume element "v". The force on the Rouse spring is given by f = br Dr, where Dr is the extension of the Rouse spring (here xi since we consider extension in the x-direction only), and br is the Rouse spring constant. Then,szx = (br/v) S zi xiThe shear stress in volume element "v" varies spatially as well as with time. The average shear stress due to thermal fluctuations is 0, <szx> = 0. The motion of the Rouse spring element "i" along the z and x directions are independent. Also, the extensions of springs in different chains in the volume "v" are uncorrelated. Then,<szx(0)szx(t)> = (br/v)2 S <zk,l(0) xk,l(0) zk',l'(t) xk',l'(t)>where the summation is over x and z extensions of all springs l on all chains k and x and z extensions of all springs l' on all chains k', i.e. there are 4 summations. This reduces to,<szx(0)szx(t)> = rc v (br/v)2 S<xl(0) xl'(t)> <zl(0) zl'(t)>since the extension of springs are uncorrelated between chains. rc v is the number of chains in the volume "v". As previously stated, the response of a Rouse bead in a single direction, zl, to a single Rouse mode, m, is given by ,zl = Zm cosdmland spring extension is governed by the derivative, zl = -Zm dm sindml, and for the x-direction, xl = -Zm' dm' sindm'l. Then <xl(0) xl'(t)> = S<Xm(0) Xm'(t)>sindml sindml' dm2, and <zl(0) zl'(t)> = S<Zm'(0) Zm''(t)>sindm'l sindm'l' dm'2 . The summation of "sin" terms only has a value at m = m' since other "sin" terms will be out of phase for an infinite chain and will be substantially out of phase for a finite but long chain. Then the two summations over the sin terms from the equation for <szx(0)szx(t)> above just yield (NR - 1)2/4 where the 4 accounts for duplication of half of the modes for each of the two "sin" term summations that are multiplied. Then,
<szx(0)szx(t)> = rc v (bR(NR - 1)r/(2v))2 Sdm4 <Xm(0) Xm(t)><Zm'(0) Zm'(t)>
Previously we had that <Xm2> = <Zm2>= (kT/2) (4/(dm2 bR (NR-1))) so,
<szx(0)szx(t)> = rc (kT)2/v S{<Xm(0) Xm(t)>/<Xm2>}{<Zm'(0) Zm'(t)>/<Zm2>}
As given above, the fluctuation dissipation theorem states that,
<szx(0) szx(t)> = kT G(t)/v
so, by comparison,
G(t) = rc kT S{<Xm(0) Xm(t)>/<Xm2>}{<Zm'(0) Zm'(t)>/<Zm2>}
Then the modulus of a Rouse chain is proportional to the temperature (as in rubber elasticity) and the molecular basis of the modulus is time dependent thermal fluctuations of the chain as described by the x and z time correlation functions. The tiem correaltion functions were previously given as being of an exponential form,
<Xm(0) Xm(t)> = <Xm2> exp(-t/tm), and <Zm'(0) Zm'(t)> = <Zm2> exp(-t/tm)
so,
G(t) = rc kT S exp(-2t/tm)
where the summation is from m = 1 to m = NR - 1. All Rouse modes contribute to the time dependent shear modulus equally. The relaxation rates in the shear modulus are increased by a factor of 2 since there are two exponentials contributing to the shear modulus arising from the x and z displacements.
If we use the previous result that tm ÅtR/m2, i.e. the high order (short time) relaxations have very small tm's, and make the Rouse steps infinitely small so the summation becomes and integral, we have,
![]()
where u = m (t/tR)1/2. The integral of the Gaussian (exponential squared) is 1 and we have,
G(t) Å t-1/2
This scaling law can be verified experimentally as a characteristic of the Rouse behavior, Strobl's figure 6.6 below.
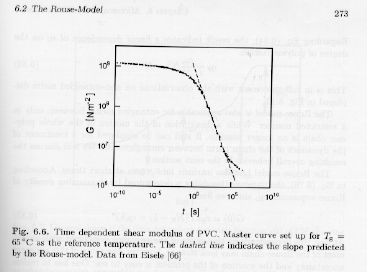
For Strobl's figure 6.6 the curve has been shifted to the glass transition temperture.
Using the frequency dependent form of the fluctuation-dissipation theorem (or by transformation of the linear response equations) the frequency dependence of the storage modulus can be obtained.
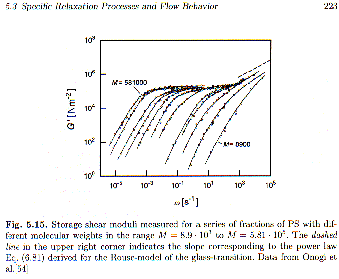
G'(w) Å (h0w)1/2
which can be experimentally verified experimentally, dashed line at high frequency in Strobl's figure 5.15.
As presented previously, the zero shear rate viscosity can be determined from the integral of the time dependent modulus,
![]()
Since it was previously shown that tR Å N2, and because the chain number density, rc, is proportional to 1/N, this integral leads to,
h
0 Å Nin agreement with non-entangled melt behavior.
Dielectric Normal Modes:
Strobl's figure 6.7 shows a schematic of the contributions of dielectric relaxations at different time scales to the time dependent dielectric constant e(t).
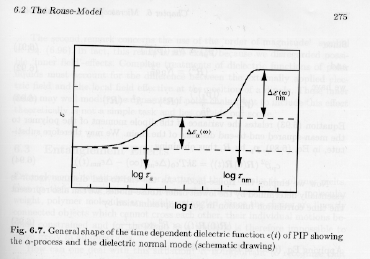
The polarization associated with the normal mode relaxation Denm, can be written in terms of a subvolume element, pv, as previously, or in terms of the Rouse chain, pp,
<pv(0)pv(t)> = v rp <pp(0)pp(t)>
For the Rouse chain polarization the fluctuation-dissipation theorem becomes,
r
p <pp(0)pp(t)> = 3kTe0(Denm(°) - Denm(t))The relaxation strength due to the normal modes, Denm(°), is given from,
r
p <pp2> = 3kTe0Denm(°)<pp2> is given by NR <(plparallel)2>, and NR = <R2>/aR2, so,
<pp2> = <(plparallel)2><R2>/aR2 = b2<R2>
Substituting this in the equaiton for <pp(0)pp(t)> above,
r
p b2 <R(0)R(t)> = 3kTe0(Denm(°) - Denm(t))It was previously determined that the end-to-end vector is determined by the lowest order Rouse modes so,
<R(0)R(t)> Å R02 exp(-t/tR)
Using this we have,
e
0Denm(t) = rp b2 R02 (1 - exp(-t/tR))/(3kT)Since R02 is proportional to N and rp is proportional to 1/N then the magnitude is independent of molecular weight while tR is proportional to N2 since it is related to the first mode or Rouse relaxation time as previously observed for normal mode relaxations.
The complex frequency dependent normal mode dielectric relaxation can also be calculated, e0Denm*(w) using the Fourier relationship between the frequency dependent and time dependent dielectric relaxations,
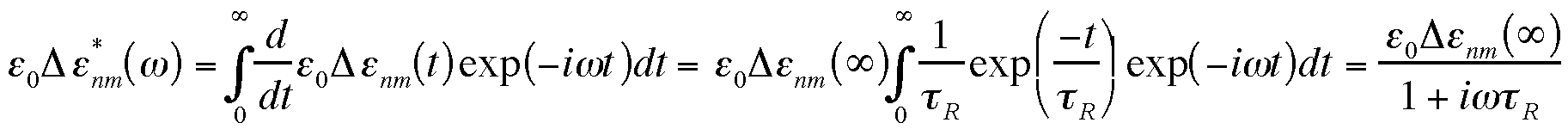
The Rouse model predicts a Debye Dielectric Relaxation process.