(from Masao Doi "Introduction to Polymer Physics" Chapter 5.)
A simple dumb bell is composed of a harmonic oscillator, a spring, with a spring constant k who's potential energy is described by U(x) = kx2/2, with viscous balls at the ends, that display a dissipative law, dx/dt = -(dU/dx)/z, where z is a friction factor associated with Stokes Law for the ball, z = 6phsa. Consider that the balls are subjected to a random thermal motion, g(t) so that the equation of motion or the Langevin equation for a ball becomes,
dx/dt = -(dU/dx)/z + g(t) = -kx/z + g(t)
The solution to a differential equation of this type, i.e. the functional form of x(t), is found from the following integral,
![]()
This is a functional expression for Strobl's figure 6.4
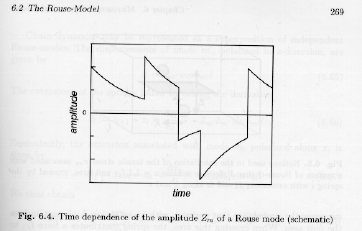
That is, a series of random pulses, g(t) lead to the jagged edge form that is followed by an exponential decay. The overall motion x(t) is a summation of these random motions and exponential decays.
The time correlation function for Brownian motion in a simple harmonic oscillator is given form this integral expression,
![]()
The time correlation function of g(t) that describes random Brownian motion is given by <g(t1)g(t2)> = 2D d(t), where t = t1 - t2 and d() is the delta function, whose integral is 1. Additionally, the Einstein relation gives that D = kT/z for this system. Using these equations the time correlation function has a simple form,
<x(t1)x(0)> = kT exp(-t/t)/k
where t = z/k. For t => 0 <x2> = kT/k. These results parallel those for the Rouse chain.