Lab 4: Laue Patterns
Laue's from 2000 Lab,
NaCl.gif,
Germanium.gif,
Silicon.gif,
Vanadium.gif
Greninger.gif,
View all 1999 Laue photos
Objective: To become familiar with the back-reflection pattern from single crystal samples using a polychromatic source.
Background: Cullity and Stock: Chapter 16 p. 471 (method
used in lab); Chapter 8 p. 263 (camera and optics); Chapter 3 p. 107 photos
and overview.
Old Cullity (Cullity pp. 92 (Chapter 3), pp. 249 (Chapter 5), pp. 233 (Chapter 8)).
Bragg's Law provides a strict set of geometric requirements for observation of a diffraction peak. For a Bragg reflection to be observed a single arrangement of geometry, dhkl,
qhkl and l must be achieved. If a monochromatic beam hits a single crystal arranged in a particular geometry with the camera it is unlikely that a diffraction peak will be observed. Laue patterns involve a single crystal sample (single crystals larger than the incident beam), and a polychromatic source which is usually unfiltered radiation from an x-ray tube. By using polychromatic radiation most Bragg reflections from a single crystal sample can be accessed just as most reflections are accessed in a powder pattern by variability in orientation of the polycrystalline sample. Figure 3-10
on pp. 108 shows two Laue patterns in reflection and transmission for a single crystal of aluminum. We will produce similar patterns in this lab.
The analysis of Laue patterns involves understanding that the diffraction spots are arranged in arcs (hyperbolas) and ellipses in the diffraction pattern. The measurement can be conducted in a forward or backward geometry depending on the placement of the film with respect to the samples. We will use back scattering in this lab since the samples are metals with low transmission coefficients. In backscattering only hyperbolas (arcs) are observed as shown in figure 8-1 pp. 264
and 3.10 p. 108. The center of these arcs or circles of diffraction spots correspond to the zone axis of a series of planes of a zone. Planes of a zone are planes which have a common direction, the zone axis, lying in all of the planes. You can think of these planes in analogy with the pages of a splayed book where the book binding is the zone axis. If the book binding is pointed at the center of the ellipse of figure 3-10
(a), and the pages are reflective, light reflecting from the pages will form an
ellipse of reflection spots, one for each page. This is shown on pp. 108 in figure 3-11. By identification of zone axes it becomes fairly simple to align single crystals for identification of crystal planes using Laue patterns and Wulff nets. This will be done for Al, Ge and Si in this lab. The latter two are diamond cubic crystal structures while the first is an FCC structure as discussed in the last lab.
Since Laue patterns involve single crystals, the natural stereographic projection is the Wulff Net as discussed in lab
3. Chapter 16 on p. 471 describes determination of crystal orientation using Laue patterns. We are only interested in the back reflection method which uses a Greninger chart, pp.
471 (also see
web link). The angles
g and d which are used in the Wulff net to determine the location of a plane normal, figure
16.4, p. 476, are determined from a diffraction spot on the hyperbola of reflection following the schematic of figure
16-4 on p. 476. AB is the projection of the plane normal on the film which is a
geometric construction and is not observed. Only the arc HK is observed and it
will appear as a series of spots. (Remember that the beam in figure 16.1 p. 472 comes through the film and is reflected back and that the wavelength of the radiation is not known so that Bragg's law can not be used.) g and d for the plane normal are related to the angles s and m
of the observed diffraction spot by the trigonometric equations on p. 474. The angle of tilt for the zone axis, f, is 90°-g, as shown in figure
16-2 on p. 473.
The Greninger Chart is a simple trigonometric tool to determine
g and d for a fixed sample to film distance. (If you were using a 2-d detector the problem of determining g and d could be solved mathematically using the equations which generate the Greninger Chart, pp.
475.) The Greninger chart shown on p. 475 can be Xeroxed on a transparency and used for a sample to detector distance of 3 cm. A new chart must be generated for different sample to detector distances. (2s is 2q for the diffraction peak and tan m is x/y for the Cartesian coordinates of the diffraction peak.) The Greninger Chart gives directly the two angles needed to plot poles on the Wulff net. It is critical to keep track of the relative arrangement of the sample to the film, if photographic film is used then this is achieved by cutting the corner of the film. For Polaroid film you must make a note of the arrangement of the face of the film in the camera.
Things to do:
- Obtain Laue reflection patterns from Si, Ge and Al (or the single crystals which are available).
- Identity the hyperbolas on the patterns by tracing the patterns on to tracing paper. Identify as many hyperbolas as possible with dashed lines (some may be straight lines) and Roman Numerals. Identify points where hyperbolas cross by letters (these are low-index planes which are in many zones).
- Identify the N-S axis of the film by a vertical line through the center of the pattern.
- Use rotation of the tracing paper, by
e, on the Greninger chart to achieve coordination of hyperbolas of constant g with one of the hyperbolas from the film. Record the angle of rotation, e, bottom of Greninger chart, and the value of g for this zone. Repeat for each hyperbola on the film.
(Figure 16.4 p. 476) You should have a
table of I, II, III etc. and values for e
and g for each.Measure the angle d for the low index planes of the pattern.
(Figure 16.4 p. 476) You should have a
table with I, II, etc, 1, 2, 3 etc (for the points),
d and g
for the bright spots.Construct a Wulff Net on a sheet of tracing paper as in Lab 3. Rotate the tracing paper by the angle e for one of the zones and mark the zone axis as a pole on the Wulff Net offset by
g as shown in Figure
16.9 on p.
482. Repeat this for all zone axis which you have identified and label all poles.
Trace the great circles for the zone axis you have plotted. The intersection of these great circles (intersections of planes with the sphere of projection) should correspond with the low index planes from the diffraction pattern. Locate and identify the low index planes as shown in
Figure
16.9 on p. 482.
Use the Wulff net to measure the angles between zones and poles using your labels. In Lab
3 you were given some tables of standard index planes for cubic systems. Use these, by trial and error, assign a consistent set of indices to the zone axes and poles of planes. Record these in your notebook.
Determine the [uvw] direction of the projection. Measure the angles between the center of the projection and three prominent low-indices poles or zone axes. This angle is related to the direction of the center of the projection by three equations of the type,
Angle Between [u1, v1, w1] and [u2, v2, w2]
(or two planes by substituting h, k, l for u, v, w)
For A Cubic System (see Appendix A3-3 pp. 502 for others)
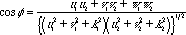
Through repeating this for three angles u1, v1, and w1 can be determined.
You should identify the orientation of all of the crystals studied (do at least 2 of the samples).
Compare a pattern from one of the single crystal samples with the Nickel filter inserted for comparison.
Use the shareware given on the xrd web page to calculate several of the Laue patterns measured or for those taken from the web data.
Questions:
- Why can't the Laue method be used effectively on polycrystalline samples? (Can Bragg's law be used for polychromatic radiation? What will the meaning of hyperbolas in a polycrystalline sample be?)
- Make some comments on the crystal quality noting p. 503, chapter 17 of Cullity/Stock.
- How did the patterns with and without the nickel filter compare?
Link to C/S Figures