Ising Model Simulation
-Write a computer program that simulates the Ising Model (2D)
using the Metropolis method described at
http://ace.acadiau.ca/science/phys/ising/.
-Try your code on 10/10 2D matrix then on a 100/100 matrix for
various temperatures 0, 0.1, 0.2, 1 (find the critical
temperature).
-Modify the program for simulation of a 3D model using the same
approach and a 10x10x10 matrix for the same temperatures.
Find the critical temperature and compare this with the
2D critical temperature.
-Modify the program for a 1-d simulation of a polymer chain
(polyethylene) using the 9 rotational isomeric states from pentane
to generate the lowest energy chain conformation for a chain of
length N. Find the critical temperature for a planar zig-zag
conformation. This is the simulated crystallization
temperature.
Possible approach:
The Ising Model employs the Metropolis algorithm in order to show
that the overall energy of the lattice is converging. The
Metropolis algorithm involves flipping a random lattice point, and
determining if the net energy decreases. If the energy does
decrease because of the random flip, then the new state is allowed,
and the simulation continues. If the new lattice configuration
causes the overall energy to increase, then a random number between
0 and 1 is generated. If the exponential of the temperature
and change in energy is less than this randomly generated number,
then the state is allowed, and the simulation continues. If this
exponential is less than the randomly generated value, the flip is
not allowed, the flipped lattice point is returned to its previous
state, a different random lattice point is chosen and the simulation
continues.
Here is the Metropolis Algorithm in step form:
1. Flip the spin of a random lattice point, creating a new
state
n'.
2. Compute DE = En'
- En.
3. If DE < 0, then the
new state is allowed and the algorithm repeats.
If DE > 0, a
random number x between [0,1] is chosen.
If e-bDE > x, then the
new state is allowed and the algorithm repeats.
If e-bDE < x, then the
state is rejected, the flipped lattice point is returned to its
original state, and the algorithm repeats.
Also See:
http://bartok.ucsc.edu/peter/java/ising/ising.html
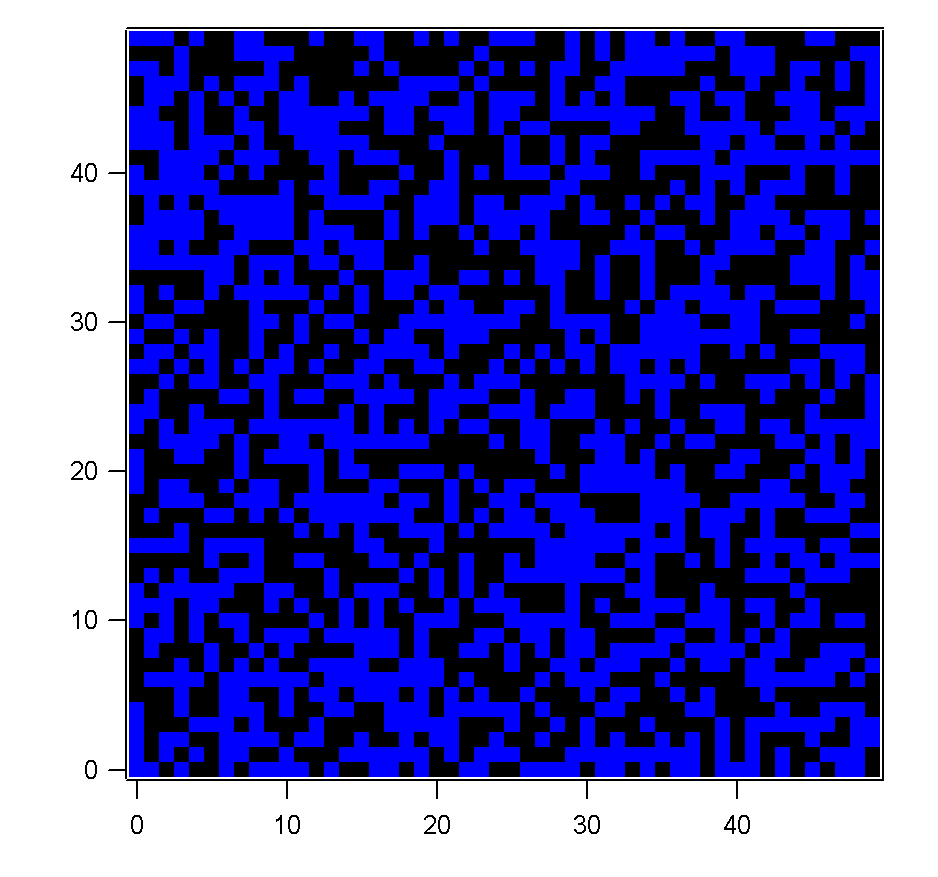
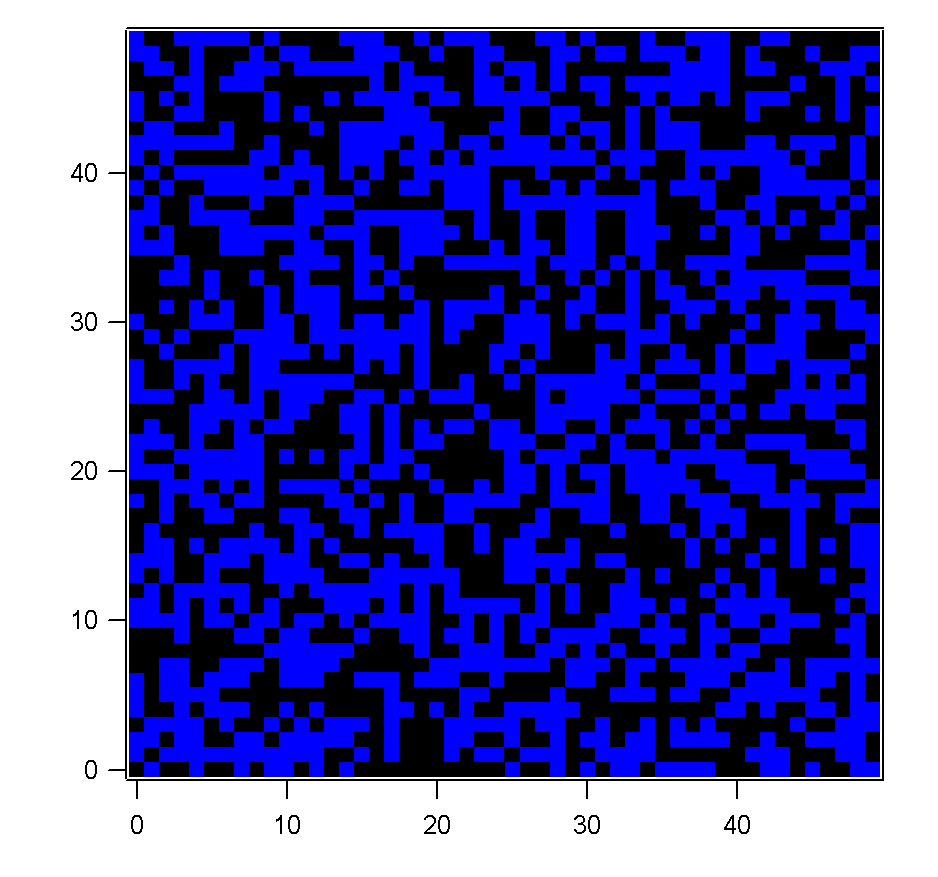
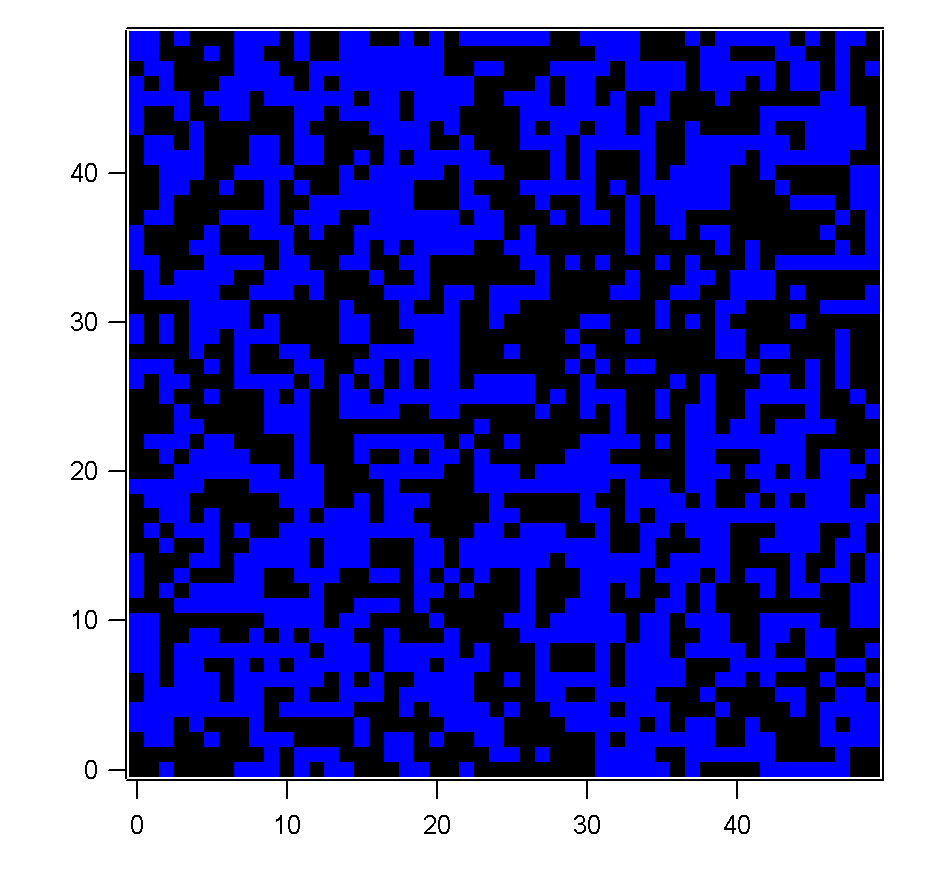
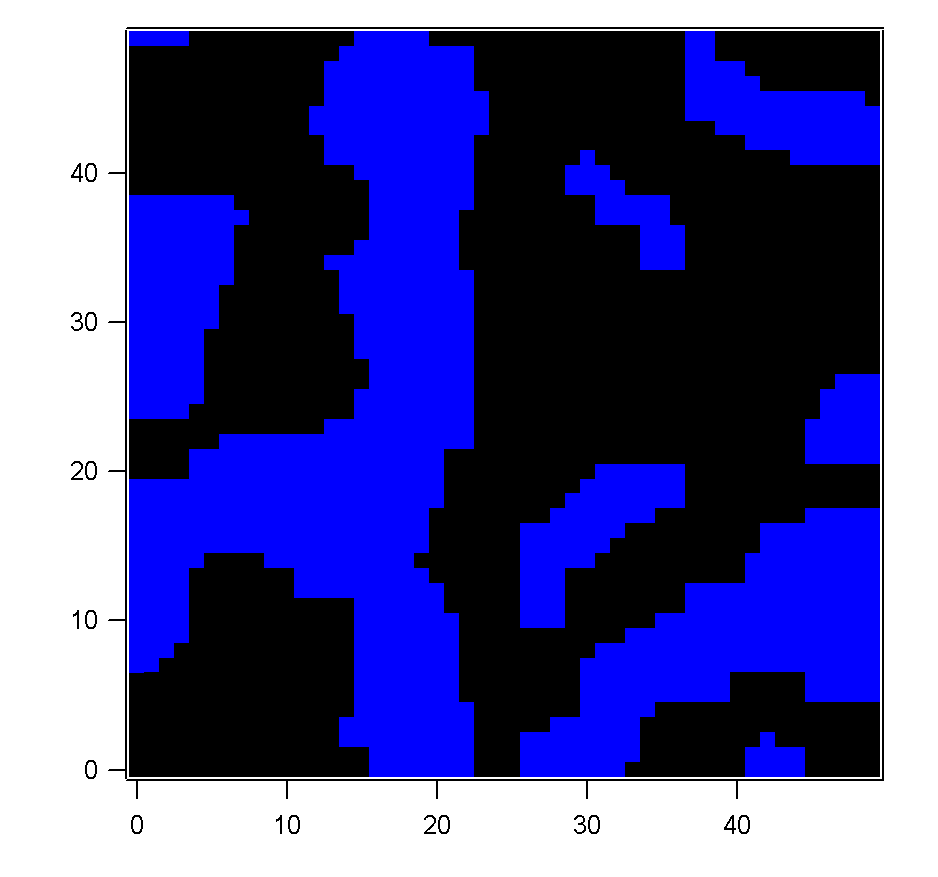
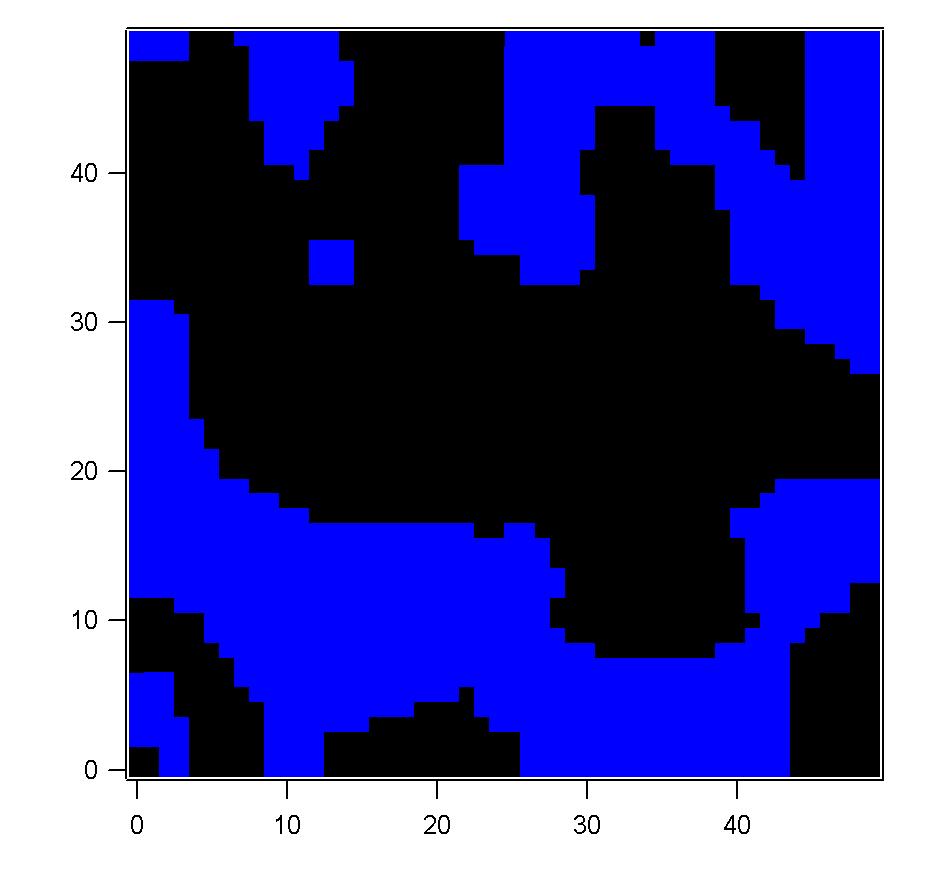
Figure 1 showing results using the above routine for the Ising
Metropolis simulation. Random start, T = 1, T = 0.2, T =
0.1, T = 0. 5000 steps, 50x50 grid.









