1. State if the following are true or false:

(a+b)+c=a+(b+c)                    (a-b)=a+(-b)                            a*b=abcosq

(ma)*(nb)=mn(a*b)                 a*(b+c)= (a*b)+(a*c)             if a┴b then a*b=0

axb*c=a*bxc                           (ma)x(nb)=mn(axb)                  ax(bxc)≠(axb)xc

bxa=-(axb)                               c=axb where c is ┴ to a and b 

2. Determine in rectangular Cartesian form the unit vector which is parallel to the vector v=2i+3j-6k where i, j, and k are unit vectors.
3. Determine in rectangular Cartesian form the unit vector which is along the line joining points P(1,0,3) and Q(0,2,1).
4. Show that if the vectors a, b, and c are linearly dependent then a*bxc = 0. 

u = 3i + j - 2k

v = 4i – j - k

w = i – 2j + k

5. Let the axes Ox₁x₂x₃ and Ox’₁x’₂x’₃ represent two rectangular Cartesian coordinate systems with a common origin at O, as shown below:

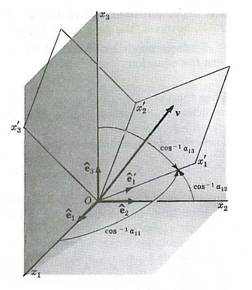
Derive an expression to relate one set of coordinates to the second if the second set of coordinates is merely the first set of coordinates rotated about the origin.