Aggregate Growth:

Mass-fractal aggregates are partly described by the mass-fractal dimension, d_f, that defines the relationship between size and mass,

where a is the lacunarity constant, R is the aggregate overall size and N is the number of primary particles in an aggregate. The mass-fractal dimension ranges from 1 to 3 in 3-d space. The growth of aggregates was first modeled using computer simulations in the 1980-90's. Some discussion of the approaches and results form these simulations will be given below. The Smoluchowski equation can also be modified for mass-fractal aggregation and this is of the most flexibility since generalized results and conditions can be determined. Additionally, self-preserving distributions have been determined for the Smoluchowski approach that enable a general treatment of mass fractal aggregation.

Simulations of Nano-Particle Aggregate Formation:

The growth of aggregates can be simulated by making simple assumptions concerning transport of particles to the growing agglomerate and the events which occur when a primary particle or cluster collide with the growing aggregate. Depending on the relative kinetics of these two processes, growth can be diffusion limited, similar to the original Smoluchowski equation, or reaction (collision) limited. Additionally, one can consider only monomer/cluster collisions or include cluster/cluster collisions as growth proceeds, such as might be expected in the free molecular range. If one considers the primary particle as a point object, then the fractal dimension of the growing aggregate should increase form a 0 dimensional point object to a 1 dimensional linear structure, to a branched chain of dimension on the order of 2 as growth proceeds. The increase in dimension with growth is a natural consequence of the persistence of velocity for nano-particle Brownian motion combined with the random path of the colliding particles. The branch content of the growing aggregate should be a function of l_pa.

As growth proceeds, the presence of branches and the convoluted shape of the growing aggregate, reminiscent of the Brownian path of the colliding particles, shields the interior bonding sites from further growth. For this reason three-dimensional growth is not possible, except by internal rearrangement. Then we can consider that an asymptotic mass fractal dimension is approached in time that is a function of the persistence of the colliding particle velocity, l_pa, and the degree to which monomers dominate over cluster transport. The latter issue is related to the diffusion coefficient in the media and thus, the Knudsen number. In all simulations of mass-fractal aggregation an asymptotic dimension has been observed at long times. This means that the overall density of the aggregate, N/R³ ≈ N^(1-3/df) diminishes with time in the asymptotic range since N is a monotonically increasing function of time.

Diffusion Limited Aggregation:

In the simplest simulations, P. Meakin (1980’s) of diffusion limited aggregation aggregates of dimension 2.5 are produced by fixing an initial primary particle at the origin of a three-dimensional lattice and allowing a random walk of primary particles, one at a time, randomly released from the edge of the lattice until either collision or loss of the particle from the fixed volume lattice occur. Despite the simplicity of this model, the dimension 2.5 is repeatedly seen in aggregates produced with low primary particle concentration and high reactivity towards bonding. The persistence of velocity is the same as the primary particle size in this case. The cluster is immobile compared to the primary particle, so this could be considered either continuum transport or free molecular transport for the monomer and continuum transport for the aggregate.

If the concentration of primary particles is higher, and cluster cluster aggregation is allowed the mass-fractal dimension is reduced to 1.8 for diffusion limited aggregation simulations. These simulations are conducted by randomly distributing primary particles on a lattice, and allowing all primary particles to collide and form aggregates which also move by Brownian motion and further aggregate to form low dimensional branched structures. The persistence of velocity is constant in these simulations regardless of particle mass, l_pa = d_p. Additionally, variation in diffusion coefficient with particle mass is not accounted for so this simulation might reflect free molecular conditions for both agregates and primary particles.

The extreme of persistence of velocity is a ballistic growth simulation where primary particles follow a linear path to the growing aggregate. For ballistic, monomer-cluster growth, similar to the first simulation discussed, three-dimensional aggregates are produced. If cluster-cluster aggregation is allowed, similar to the second simulation above, mass-fractals of dimension 1.95 are produced. For this case the persistence of velocity for monomers and aggregates is larger than the lattice diameter.

When persistence of velocity relative to primary particle size and variability of the diffusion coefficient with particle size and transport regime are considered in more complicated simulations the results are qualitatively similar to the simple simulations mentioned above. In the free molecular range Mountain found values of df of 1.89 to 2.07 for diffusion limited cluster-cluster aggregation, for instance.

The aggregates that are produced by computer simulation are not monodisperse in N. Generally, the mass distribution of aggregates reach a self-preserving form indicating that an analysis based on the Smoluchowski equation as done for coagulation may be possible for aggregation as was done by Friedlander and is discussed below.

Reaction Limited Aggregation Simulations:

A sticking probability can be introduced into simulations to account for the probability of a particle or cluster bonding with the growing aggregate on impact. The importance of a stinking probability is that a particle just after collision that does not stick has a much higher probability to transport by Brownian motion to the same or another local site on the aggregate. Then the colliding particles can probe the surface of the growing aggregate. Additionally, colliding particles can become “trapped” by high coordination number regions of the aggregate since translation away from a site bounded by multiple aggregate subunits has a lower probability. The net effect of a sticking probability is to allow a type of local rearrangement towards multiply coordinated bonding. This directly leads to higher dimension aggregates. For primary particle-cluster growth with a low sticking probability three-dimensional aggregates are formed. If cluster-cluster aggregation is allowed a mass-fractal aggregate is formed with a dimension of 2.09 which is larger than that observed for diffusion limited aggregation (1.8).

Other Dimensional Descriptions of Mass Fractal Aggregates:

The mass-fractal dimension, together with the aggregate size, and primary particle size yield a partial description of a mass-fractal aggregate that is sufficient for the study of some aspects of growth and some properties, especially those related to mass/volume ratios. However, the mass-fractal description is not intended to be a complete description. For instance, given the mass-fractal dimension and size information it is not possible to reconstruct a facsimile of the aggregate without making assumptions concerning the branch content. If you are told that an object has a size of 100nm and is composed of 1 nm primary particles with a dimension of 2 the object could range from the regular object, a disk of thickness 1 nm and diameter 100nm with 10,000 primary particles, to a linear chain of diameter 100nm composed of 1 nm steps on a random path that is composed of 10,000 steps. From the mass-fractal dimension there is no possibility of distinguishing between these objects.

Dimensional analysis can be used to describe a variety of features beyond the mass-size scaling. For instance, the spectral dimension is used to describe the energy distribution in a mass-fractal object, the chemical dimension is used to describe the reactivity of a mass-fractal structure and the connectivity dimension is used to measure the branch content of a mass-fractal structure. The number of primary dimensions that could be defined for a given object is only limited by the number of observable features that exist for the object. A primary dimension reflects a fundamental scaling feature for an object. One feature of a primary dimension in three dimensional space is that the value is equal to the mass-fractal dimension for regular objects and its value is equal to or less than the mass fractal dimension for fractal objects. Because of the wide range of dimensions that can be defined for various systems, the field of dimensional analysis based on fractal concepts is challenging to understand. Nonetheless, at least two dimensional values are necessary for even the most rudimentary understanding of aggregation, i.e. in order to distinguish between a disk and a linear random walk.

If we consider branching in mass-fractal aggregates, a natural measure of the object is the minimum path or primitive path, or number of steps, required to traverse the object between the furthest points in the aggregate, L. For a disk, L is the diameter of the disk, while for a linear random walk with no branching, L is the degree of aggregation, N. The scaling between L and N yields the connectivity dimension, C, for the aggregate,

L^C = BNl

Where B is a scaling prefactor similar to the lacunarity for mass-fractal scaling. For a linear chain L ≈ N so C = 1. For a disk L² ≈ N so C = 2 = d_f. C is a primary dimension. The number of branches, n_br, in a mass-fractal aggregate can be determined from C since,

n_br ≈ N/L

The average coordination number for monomers in the aggregate, c_N, is given by,

c_N = n_br/N ≈ 1/L

The average coordination number can be determined from simulations and it is found to reach an asymptote in fractal growth.

The mass-fractal and connectivity dimensions are not independent in the sense that branched objects of the same path dimension have a larger mass-fractal dimension. For example a linear, Gaussian chain has a mass fractal dimension of 2 and a connectivity dimension of 1. For a randomly branched chain that follows a Gaussian path the mass fractal dimension is 2.5 and the connectivity dimension is close to 2.

Application of the Smoluchowski Equation to Mass Fractal Aggregaton:

The Smoluchowski equation translates the problem of calculating particle growth rate, dn/dt, to the problem of determining the collision frequency function, b_ij. For single particles in the free molecular range,

where the single underlined part corresponds to the collision cross section for i and j aggregates and the double underlined part corresponds to the average relative velocity between agglomerates. b_ij.reflects the average hydrodynamic volume swept by the two agglomerates. For the free molecular regime the aggregate is completely draining and the hydrodynamic volume of the aggregate is N_agg v₀ where N_agg is the degree of aggregation and v₀ is the volume of a primary particle,

R is the “hydrodynamic radius” of the aggregate for the continuum range, i.e. non-draining range. In the continuum range the aggregate, with respect to diffusion, is a sphere like object. So while the velocity depends on a Rouse like model, f_agg = N_aggf₀, the aggregate cross section is viewed from a non-draining hydrodynamic perspective. The reason for this is simple, if the aggregates are rigid structures, then penetration between aggregates is unlikely, especially when d_f ≥ 2, while, small molecules can easily penetrate the aggregates in the free molecular range. This picture breaks down when d_f < 2 since it rapidly becomes possible for aggregates to penetrate the hydrodynamic sphere of each other, for instance the hydrodynamic sphere for a rod is a sphere of diameter L. Two rigid rods can easily penetrate each others hydrodynamic radius by lining up. This is not true for d_f ≥ 2. Additionally, the projected cross section of an object of d_f < 2 will depend strongly on the orientation of the object. Again this is not necessarily true for a random mass-fractal object with d_f ≥ 2.

As was shown earlier, the calculation of the diffusion coefficient for a mass-fractal aggregate requires, a priori, a value for the mass fractal dimension. The calculation using the Smoluchowski equation yields a different result than the typical goal of the computer simulations mentioned above. Most computer simulations seek to determine the mass fractal dimension and perhaps the connectivity dimension as a function of growth conditions, while the Smoluchowski equation seeks to describe the aggregate growth rate and aggregate size distribution with the fractal dimension as an input parameter.

The collision cross section, single underlined term above, is determined by the average fractal scaling,, for fractals of dimension between 2 and 3,

Substituting for the mass of the aggregates in the first equation and this expression for the cross section we have,

Free Molecular Regime

where . For the continuum regime the collision kernel is,

Continuum Regime

where dpi is the collision diameter for the agglomerates. For fractal aggregates we have,

D ~ D₁/N_agg = (d₁/d_agg)^df D₁ Free Molecular Range

D ~ D₁/N_agg^1/df = (d₁/ d_agg) D₁ Continuum Range

and for large aggregates the continuum regime is used so,

Continuum Regime (N>>1000)

Self-Preserving Aggregate Size Distributions:

The collision kernels give above are homogeneous functions of the colliding aggregate volume,

Free Molecular

for the continuum regime l = 0. Since the kernels are homogeneous the distributions reach an asymptotic self-preserving distribution. The self-preserving equation is given by,

v is the solids fraction of the aggregate, and f is the volume fraction of solids in the system.

The particle number density, N_∞, decays with,

using the free molecular regime collision kernel given above, and the self-preserving number distribution give above,

and "a" is an integral function of the self-preserving distribution function above. Values for a are given by Friedlander from Monte Carlo calculations,

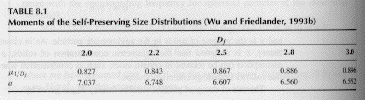
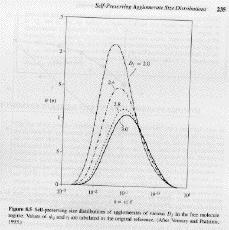
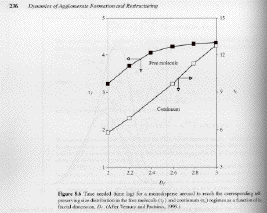
Aggregate self-preserving distributions solved using a discrete sectional model are shown in the figure above (Vemury and Pratsinis). The time to reach the self preserving size distribution was also calculated by Vemury and Pratsinis and is shown in the figure below. In both cases the self-preserving limit is reached faster than spherical clusters.