Chapter 2. Nano-Powders: Surface Growth of Nano-Clusters

Consider a general scheme for production of nanoparticles. In the nucleation stage (Chapter 1) monomers are produced or added to the system by a mechanism that maintains a constant, low concentration under conditions of high supersaturation (low temperature for instance). Nucleation occurs over some time with constant monomer concentration. Eventually surface growth of clusters begins to occur which depletes the monomer supply. When the monomer concentration falls below the critical level for nucleation (critical supersaturation level), nucleation ends. The stable nuclei larger than n* can continue to grow by 2-d nucleation on the surface of the clusters since the critical supersaturation for surface growth is lower (as well be shown below) for surface growth. Eventually all growth ends when the concentration reaches the solubility limit for a bulk solid. The critical features of synthesis for narrow polydispersity and small particles are a short nucleation time period and separation of the growth process from the nucleation process and control or termination of the growth process. A general analysis of the growth process (2d surface growth) is then important to understanding nano-particle synthesis.

Surface Growth of Nucleated Particles:

When particles become large, n>>1, the model for particle growth should consider surface nucleation of a patch of height h and radius r on the surface of a particle. The free energy of formation of a disk-like patch containing n' monomers, DG', is given by,

with f = kTlnS is the supersaturation parameter for the system and y' is the additional surface energy of a 2-dimensional n'-mer associated with the sides of the patch,

where v₁ is the volume of a monomer in the solid phase, and y' is the surface energy of a monomer. So,

(This is a lower value than the corresponding cluster nucleation function, .)

The maximum of the function corresponds to the critical nucleus, n'*,

(for n-mer this was so the surface patch is smaller than the cluster) and,

(Compare with so the surface nucleus has a lower activation energy.) The critical radius, r'*, for such a patch is given by,

These results can be compared with those for a 3-dimensional nucleus,

and

The f dependence of the nucleation rate is weaker for surface nuclei.

The equilibrium number concentration of surface nuclei is given by,

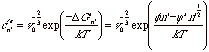
(compare with 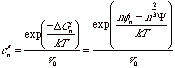) where v₀ is the volume of a solvent molecule and the -2/3 power reflects the area on the surface.

In order to compare cluster nucleation with surface nucleation and surface growth we consider the supersaturation energy parameter, f_n, that relates the concentration of monomers in equilibrium with an n-mer c_(n) to that in equilibrium with the bulk solid, c_(∞),

This differs from f which relates the actual supersaturated system concentration, c, to the concentration in equilibrium with the bulk solid, f = kTln(c/c_(∞)). The free energy of formation for a surface patch of n' monomers on a cluster of n monomers can then be written in terms of the difference in chemical potential between that for a monomer in the n-mer and the chemical potential in the supersaturated solution,

The difference in chemical potential can be calculated from ,

So,

The above expressions for n'*, DG'* and c'^e can be rewritten in terms of this reduction in the supersaturation energy parameter,

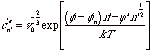
This is the lower cutoff for growth of surface patches of size n' in terms of the n-mer chemical potential, f_n. For n=>∞, f_n => 0 agreeing with the previous expression for a bulk solid.

Rate of nucleation for a surface patch, n': J'

J' can be written following a similar development to that for the n-mer nucleation rate,

a'_n'-1 is the edge area of the surface patch. The edge deposition rate constant, k_'d can be greater than the bulk deposition constant, k_d, since the side surface has a negative curvature (see Gibbs-Thompson form 2). We can propose that,

if the basic mechanism of deposition is the same for the edge of a patch and a surface of a solid. If the same development is followed for the surface patch kinetics and the n-mer surface deposition kinetics we can obtain,

This leads to the same results as for nucleation of an n-mer, at n'*, x' = 0 and the concentration of n' patches is half the equilibrium value. For higher n' there is a growing difference between the equilibrium and kinetic concentrations favoring smaller patches.

Diffusion versus Reaction Controlled Monomer Deposition on Nano-Particles.

Nanoclusters in a media such as a liquid or gas phase are subject to thermal motion or Brownian motion. The fluid at the surface of the particles is stagnant while the particle moves. In monomer deposition to a growing cluster the monomer must diffuse through this stagnant layer of thickness d. The thickness of the stagnant layer depends on the temperature (since the particles are subject to Brownian motion) and the size of the particle, r. Particles only become subject to convection as a dominant transport feature when they are larger than about 10 to 100 micron. For nanoparticles d is about 2 to 8 times r (Sagimoto, AICHE Journal 24 1125 1978). Then the bulk liquid phase can be considered to have a uniform supersaturated monomer composition, C_b, while the concentration at the particle interface, C_i, may be much lower due to the competition between deposition (reaction) and the ability to transport to the cluster surface through d (diffusion). For growth C_i should be larger than the solubility of the particle, C_r. We can consider the flux of monomers, J, passing through a spherical surface surrounding the cluster at a position x between the interface and the edge of the bulk liquid,

J is constant in x for the diffusion layer at steady state. Then Fick's law can be integrated to obtain,

At steady state, this is equal to the consumption rate of the monomer species at the particle surface,

C_i is difficult or impossible to measure so it can be eliminated from these two equations,

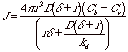
This can be converted to the linear growth rate of the nanocluster, dr/dt = JV_m/4pr²,

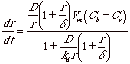
The ratio of (C_i-C_r)/(C_b-C_i) determines whether the rate limiting step for growth is kinetically determined by transport (less than 1) or is determined by reaction rate at the interface (greater than 1). We have,

For D<<k_dr, C_i ~ C_r and we observe diffusion limited growth where,

further, r/d is usually <<1 for nanocluster growth so,

Diffusion Limited Growth

The value of r/d for sub micron clusters in aqueous solutions is close to 0.25 and is approximately constant in particle size so the last equation is more correctly,

Diffusion Limited Growth (sub micron)

For diffusion limited growth the linear growth rate decreases with size.

For reaction limited growth D>>k_dr and C_i~C_b and,

so the linear growth rate does not depend on nanoparticle size.

Since the main issue is a comparison of D and k_dr, it is more likely that reaction controlled growth is observed for very small particles, i.e. when r is extremely small D>>k_dr generally and reaction controlled growth is observed which favors larger particles since the linear growth rate is independent of particle size. At some point the conditions may favor diffusion limited growth and the rate of growth will diminish with particle size. If the particles grow to greater than a few micron in size convection destroys the stagnant layer and growth rate is again independent of particle size.

Application of Gibbs-Thompson Equation:

The Gibbs-Thompson equation can be used to describe the particle size dependence of C_r for nano-clusters,

For small x, exp(-x) ≈ 1 - x + x²/2! - x³/3! +…, so for small arguments to the Gibbs-Thompson exponential (small particles) we have,

The bulk solution concentration can also be expressed in this form using a particle radius in equilibrium with the solution, r_b,

For diffusion controlled growth of nanoclusters we can write,

Diffusion Controlled Growth

where,

The rate of change in the width of the size distribution (standard deviation of size), d(Dr)/dt, can be estimated from this expression for the linear growth rate by considering the above equation for dr/dt close to the mean size <r> and taking the derivative of the rate with respect to <r>,

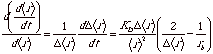Diffusion Controlled Growth

When the mean size in the distribution is less than twice the size in equilibrium with the bulk solution d(Dr)/dt > 0 and the distribution broadens with time. This corresponds with a shallow quench since the Gibbs-Thompson equation gives . However, when <r>≥2r_b, i.e. a very deep quench, the size distribution self-sharpens and becomes narrower with time, d(Dr)/dt < 0. Such self-sharpening of the size distribution has been repeatedly reported in the literature and is a desirable condition for nanoparticle growth. A deep quench in diffusion controlled growth can lead to self-narrowing particle size distributions!

The figure, below, from Sagimoto, Adv. Colloid Interface Sci. 28, 137 (1984) illustrates the expected behavior of the mean size and distribution width in growing mean particle size for diffusion controlled growth.

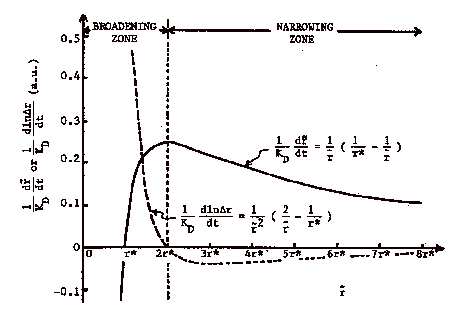
For reaction controlled growth the result of such a calculation indicates that under all conditions of supersaturation the particle size distribution will broaden. Using the Gibbs-Thompson equation we have,

Reaction Controlled Growth

with,

By taking the derivative with respect to <r>,

which is always positive. The broadening rate decreases with larger mean particle size.

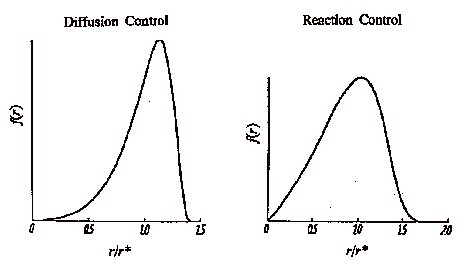
Observation of a self-sharpening particle size distribution is evidence for diffusion controlled growth. At the extremes of size the two mechanisms can not be distinguished from the rate of change of the size distribution.

Ostwald Ripening:

If two particles of different size or different crystalline phase are present in a liquid or aerosol it is thermodynamically favorable for the larger or more stable particle to grow at the expense of the smaller particle. If the system has reached a pseudo-equilibrium state the concentration in the media (liquid or gas) will be intermediate between the equilibrium concentration for the two particles. For a dissolution rate constant, k_n, for the smaller (less stable) species that is greater than the growth rate constant, K_x, of the larger (more stable) particle the pseudo-equilibrium concentration is close to the equilibrium concentration of the larger (more stable) particle and the growth is governed by deposition on the larger particle. If the opposite condition exists then the pseudo-equilibrium concentration is closer to that of the smaller (less stable) particle and the growth is governed by the dissolution of the smaller species. This can be used to control the media concentration if a sacrificial phase is present to feed the growth of the more stable phase. That is, close to a constant monomer concentration could be maintained by such a process.

Ostwald ripening involves such a process and is driven by solubility differences between different particles such as governed by the Gibbs-Thompson equation. The theory of Ostwald ripening was developed by Lifshitz and Slyozov and also by Wagner so it is called the LSW theory.

If dissolution and growth reach a steady state condition the size distribution the particle size distribution, f(r,t) can be expressed in terms of the ratio between the particle size, r, and that of a particle in equilibrium with the monomer solution, r_b, r = r/r_b, and,

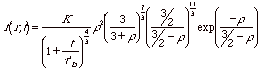Diffusion Controlled Ostwald Ripening

where t'_D is a time constant given by,

where r_b⁰ is r_b at t = 0. This equation can be used for r≤3/2. For this function the mean particle radius equals the particle radius in equilibrium with the liquid phase, r_b = <r>. r_b as a function of time is given by,

So particles grow with the cube root of time.

For reaction controlled Ostwald ripening, with first order kinetics the size distribution function for r ≤ 2 is given by,

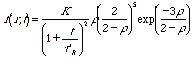Reaction Controlled Ostwald Ripening

where,

The mean radius if 8/9 of r_b, and r_b(t) is given by,

so the mean particle size grows with the square-root of time.

C. Wagner, Z. Elektrochem. 65, 581 (1961)

Contact Recrystallization:

When two particles contact each other under conditions that encourage growth, they undergo rapid recrystallization near the site of contact. This behavior can be explained using the Gibbs-Thompson equation. For normal Ostwald ripening with two particles of size r₁ and r₂ with r₂>r₁, growth of the larger particle occurs due to the difference in chemical potential for a monomer in the large particle versus that in a small particle,

For contact recrystallization the driving force for growth near the point of contact between two particles (of the same size, r₁) is given by,

where r_2a and r_2b are positive radii of curvature for the point of contact between the particles. Two particles in contact have a strong driving force for the growth at the point of contact and this can be achieve through partial dissolution of the particles themselves.

Coagulation/Aggregation/Aggolomeration:

The last section indicated that two nano-particles that touch each other under conditions that allow particle growth will bond and ripen to smooth out the point of contact to the extent allowed by kinetics.