Particle Size Distribution Functions:
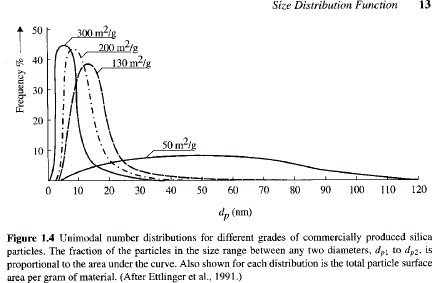
The figure above (from S. K. Friedlander, Smoke, Dust and Haze 2000) shows particle size distributions for nano-scale fumed silica. The smaller particles were produced at lower flame temperature under higher degrees of supersaturation while the larger particles show high degrees of coalescence and sintering of particles. Such particle size distributions can be obtained by hand counting TEM images, or through the use of differential mobility analysis (DMA) with fractionation. A characteristic feature of the distributions is the tail at large particle size that is predicted by diffusion limited growth at high degrees of supersaturation. Self-sharpening of the distributions at high supersaturation is evident at smaller sizes. The curves are presented as normalized number per unit volume (L3) at a particular equivalent diameter (l), dN/N (L-3),
![]()
![]()
In coagulation the total particle volume is conserved when two particles join. For studies of coagulation a distribution based on particle volume is more useful,
![]()
Since,
![]()
for a spherical particle,
![]()
and,
![]()
This can also be done for a surface area based particle distribution. There are several ways to present particle size distribution data beyond a linear linear plot shown above. Some systems display a power-law relationship between number and size, np ~ dpP, over some range of size. A plot of log np versus log dp is advantageous for such systems since the power P might be indicative of the particle formation mechanism, i.e. breakup associated with volume or mass.
Cumulative data is also of use when a particular size limit is of interest, i.e. if you desire the fractional number of particles below 1 micron. In some analytic techniques, such as sieving,the primary data is the cumulative size distribution. In such cases dV/d(log dp) might be used where V is the cumulative volume of particles between d = 0 and d = dp,
![]()
For spherical particles,
![]()
where m is the cumulative mass of the particles with constant density rp. If the primary data is given in cumulative size then it is possible to obtain the number distribution by differentiation of the experimental curve but this introduces more error than a direct measure of the particle size distribution.
Distributions can be unimodal (see above) or multimodal (typically bimodal) as shown in the sketch below of cumulative volume versus particle size (from S. K. Friedlander, Smoke, Dust and Haze 2000).
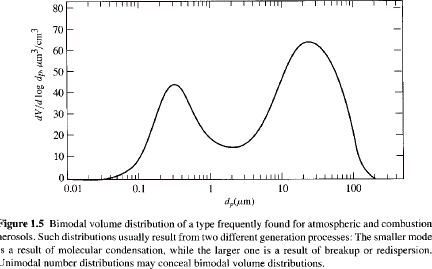
A bimodal distribution might result from a process involving breakup of large particles, multiple sources of particles or variable growth mechanisms in the system.
Moments of Particle Size Distributions:
In order to use a particle size distribution it is often desired to obtain a weighted value from the distribution. Additionally, many analytic techniques yield different moments of the distribution so it is important to consider the relationships between different moments. For instance, comparing an average particle size from dynamic light scattering with an average particle size from gas absorption measurements requires such consideration. The n'th moment, Mn, of a distribution is defined by,
![]()
The zero'th moment, n = 0, M0, is the total number or concentration of particles, N∞.
The first moment is the number average particle diameter, <dp>, times M0.
The second moment is the total surface area in the system divided by p (for spherical particles). The average surface area per particle is given by,
![]()
For large particles (relative to the wavelength of light) the second moment is proportional to the turbidity of the sample.
The third moment is proportional to the total volume (per unit volume) of the system. This is proportional to the volume fraction particles, f. For spheres,
![]()
The average volume of a particle is given by,
![]()
One use of the fourth moment is in modeling sedimentation of
particles that follow Stokes Law.
The rate that a horizontal surface is covered by settling particles is ![]() . The fifth moment is proportional to the
mass flux of particles sedimenting from a suspension,
. The fifth moment is proportional to the
mass flux of particles sedimenting from a suspension, ![]() .
.
The sixth moment is proportional to the light scattering from very small particles relative to the wavelength of light. Scattering from such a small particle is proportional to the volume of the particle squared for a constant dilute volume fraction of particles since scattering involves interference between waves from two positions in the particle and the number of such positions is proportional to the mass of the particle. The volume scales with dp6, so the integrated contributions to scattering contrast is proportional to M6. For most distributions the higher the moment the higher the normalized, linear value, i.e.
![]()
This means that light scattering from small particles will be sensitive to the larger particles in a distribution.
It is also possible to obtain fractional moments. This is common in transport based measurements such as intrinsic viscosity and aerosol convective diffusion.
Distribution Functions:
Since it is often not possible to obtain particle size data from dp = 0 to dp = ∞, it is desirable to use a function with a minimum number of free parameters to describe the particle size distribution. From such a function all moments can be calculated. If the function has 3 free parameters, for example, such as the mean, standard deviation, s, and peak value or modulus of the distribution, then three moments will be needed to describe the distribution. The most common particle size distribution is called the log-normal distribution which is based on the Gaussian distribution. A log-normal distribution is natural to a system where particles are formed or broken up in accordance with some power of particle size such as the volume or surface area. Then the system can be thought to be random (Gaussian) in the log of the particle size.
The Gaussian distribution is given by,
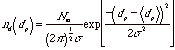
where,
![]()
Close to monodisperse particles can be described with the three parameter Gaussian distribution.
Particle distributions characterized by a long large size tail, such as those shown in the first figure of this section, can often be described by a power-law relationship between particle size and number. For such distributions a log-normal or log-Gaussian distribution is used,
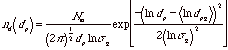
where the subscript "g" stands for geometric, and,
![]()
![]()
sg is the geometric standard deviation and dpg is the geometric mean.
Other distribution functions contain more than the three parameter Gaussian or log-normal distribuions and can describe certain skewed distribution curves. Example of these are the Lorentzian distribution and Schultz distributions.
Power-Law Distributions:
A power-law distribution has the form,
![]()
Such a distribution is usually only applied over a limited range of particle size. m is typically a negative number so the number of smaller particles falls off with the inverse of a power of particle size. The Junge distribution, m = -4, is used for atmospheric nano to micro particles in air pollution. Also, in clean room applications, particle distributions are often estimated using a power-law distribution with m = -3.2.
Scaling of Particle Size Distribution for Common
Physiochemical Processes:
The first three particle size distributions in the first figure of this section show similar shape. If the x and y axes are normalized by the integrated area and the mean particle size respectively the curves might fall on a universal curve indicating that the distributions are self-similar, i.e. that they rely on the same mechanism for their formation.