Dumbell Model for Dynamics

The dumbell model is composed of a harmonic oscillator and dissipative spheres subject to a random thermal velocity that pulses in time and can be compressive or tensile.  Only one dimension is considered, x, the separation distance between the two spheres.  Consider that the spring displays the spring constant of an isolated Gaussian chain.  (2 Quiz Grades)

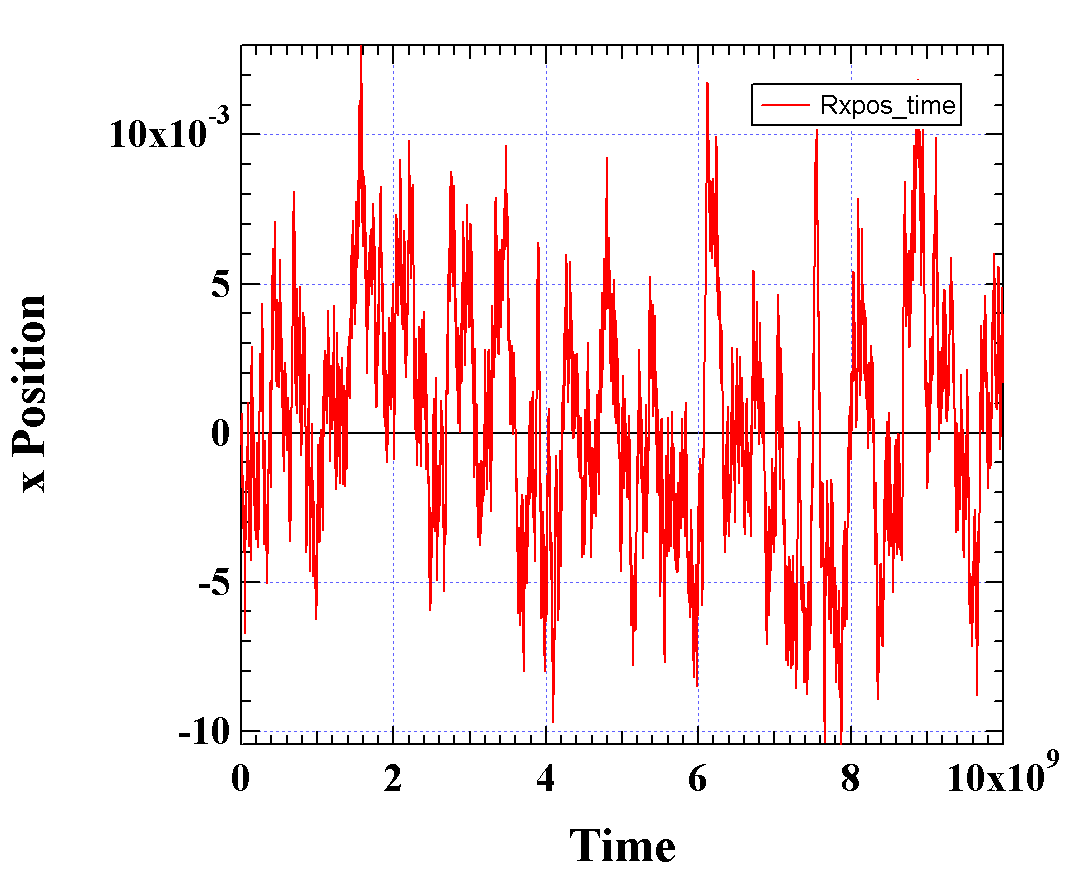
a) Simulate the dumbell model for molecular dynamics and show the average separation distance "x" as a function of time, t in a plot. 

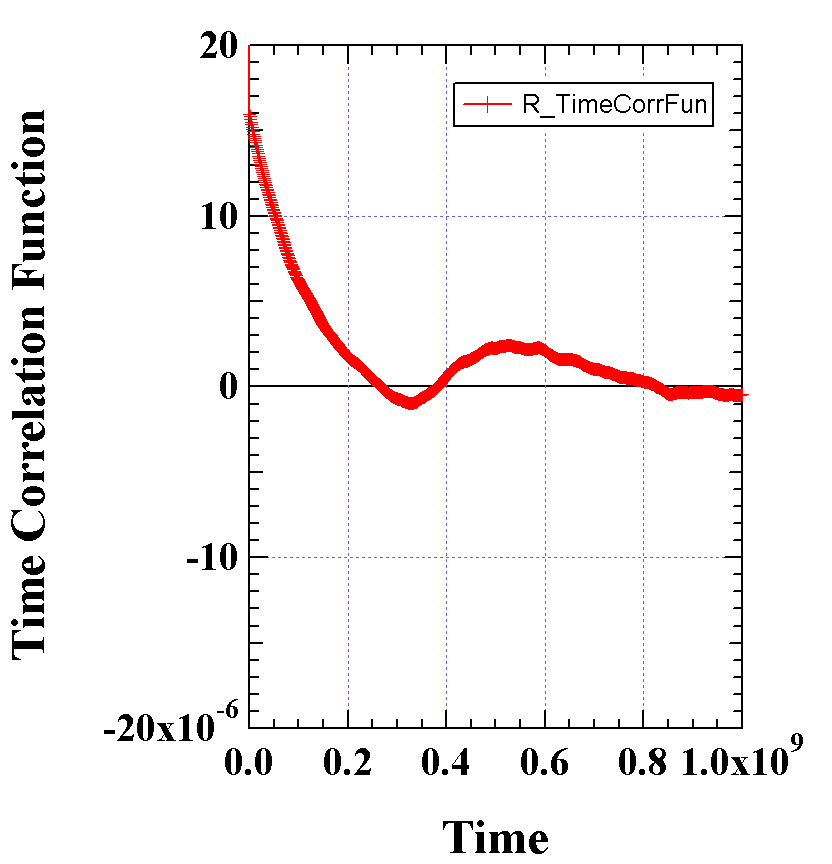
b) Calculate the time correlation function <x(t) x(0)> and plot the correlation function versus t showing an exponential decay from your calculation. 

c)  From this plot extrapolate <x(0) x(0)> and show that this is proportional to 1/k, the inverse of the spring constant. 

d) Perform a, b, c for variable chain molecular weight (spring constant k ~ 1/N), friction factor (x ~ h), and magnitude of g(t) ~ D^1/2.

e) Compare plots of <x(t) x(0)> versus t for these different conditions. 

f) Also, plot <x(0) x(0)> for these different conditions to demonstrate the dependencies of the RMS end-to-end distance on dynamic features. 

g) Comment on your findings.

A Useful web page on time correlation functions is http://www.nyu.edu/classes/tuckerman/stat.mech/lectures/lecture_21/node4.html also see class notes from this class at http://www.eng.uc.edu/~gbeaucag/Classes/Physics/DynChapter6html/DumbBellModel.html

Below are results from a simulation of 10,000 steps with time up to 1e10 for ks = 1, Friction Factor = 100 and D = 0.001.  The relaxation time is 100.