Optional Project 1: Simulation of Random Walks

-Write a computer program that simulates a random walk (100,000 steps) on a Cartesian coordinate system.  For 100 simulations calculate the mean end-to-end distance, the root-mean-square end-to-end distance and the persistence length. Compare with R² = nl².  (1)

-Modify this code to include short range interactions (avoid recent 1 to 10 steps).  (2)

-Vary the Kuhn step length from 1 Cartesian steps to 10 Cartesian steps and note the effect on the end-to-end distance.  (2)

-Modify the program to simulate a self-avoiding walk (long range interaction).  For 100 simulations calculate the mean end-to-end distance, the root-mean-square end-to-end distance and the persistence length. Compare with (R/l) = n^3/5.  (3)

-Vary the degree of self-avoidance by avoiding cells within 1 to 3 Cartesian steps from a long range position (try higher avoidance and discuss result).  (3)

-From your simulated structures calculate the root-mean-square end-to-end-distance, the radius of gyration, the pairwise correlation function g(r) and the Fourier transform of the pairwise correlation function, g(q).  (4)

-Plot g(q) versus q and compare with what is expected for a Gaussian chain and a SAW chain.  (4)

Possible approach:

Make a 3-d vector for the position of a chain unit (x(i),y(i),z(i)).

Begin simulation at (0,0,0)

Pick randomly x, y or z and increment by a random choice of +1 or -1.

Repeat previous step 99,998 times excluding a back step (for short range interaction).

-Report final end-to-end distance and store path.

-Plot the path using nih-image (scion image) program or the like. 

-Plot log end-to-end distance versus log of molecular weight showing lines of slope 1/2 and 3/5 for comparison. 

-Comment on problems with calculation of scaling dimension for a single chain, for short chains.  Specify the conditions needed to obtain the scaling dimension correctly.

For self-avoidance check each step to forbid positions already occupied by the chain.  You may need to run fewer steps to achieve self-avoidance in a reasonable time.  For larger degree of self-avoidance, forbid cells within 5 steps in any direction from an occupied position.

There are other ways to code this simulation.

Brownian part of program is one quiz grade ((1) above), short range interaction is a second quiz grade ((2) above), long range interaction is a third quiz grade ((3) above), calculation of the statistical and scattering from your simulations is a fourth quiz grade, (4) above.

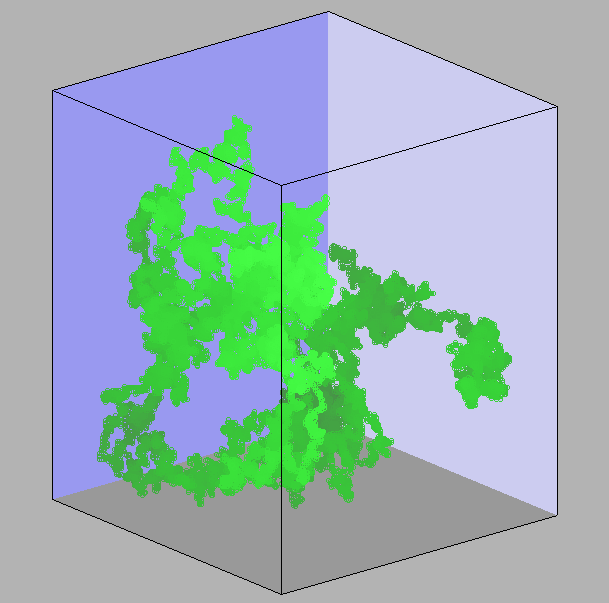
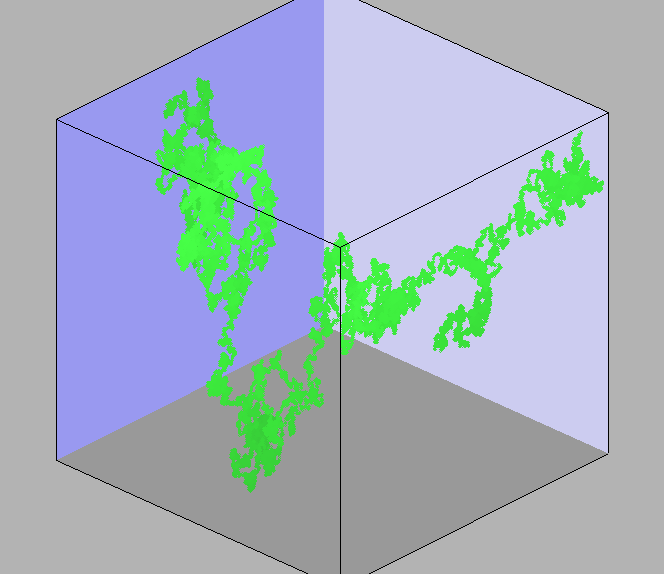
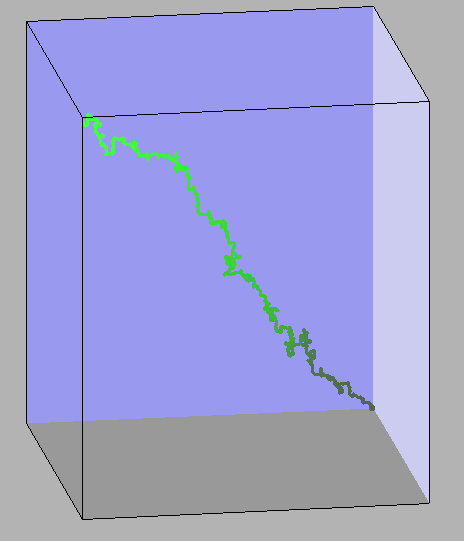
Figure 1.  50,000 setp Gaussian (left), 50,000 step SAW/SRI 1 cell (middle), 50,000 step SAW with 3 cell avoidance and 1 cell SRI (right).  50,000^3/5 = 660 and 50,000^0.5 = 224.  End-to-end distance for the Gaussian is 71, for the SAW (1 step avoidance) is 397 and for 3 step avoidance is about 5000.

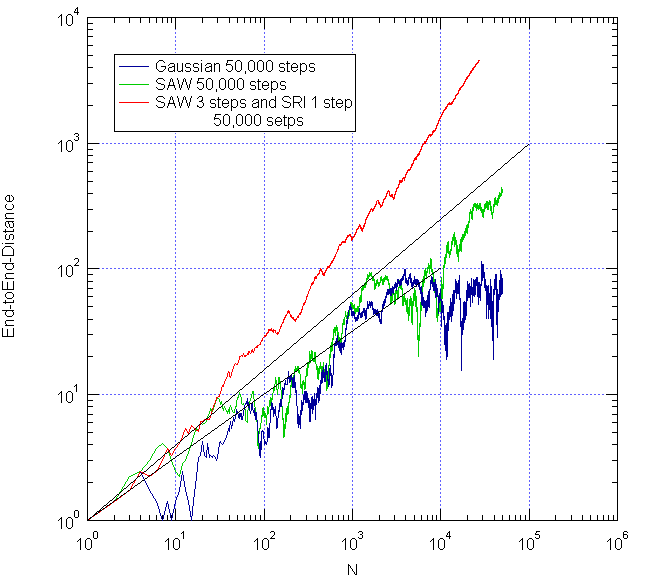
Figure 2.  R end-to-end distance versus N in a log-log plot showing lines for 1/2 and 5/3 slope.