Persistence Length, One Application of the Ising-Chain and the RIS Model.

Local features of a polymer chain such as the chain persistence, and the pair correlation function, g(r), and the associated high-q scattering function, g(q), can be calculated from a careful statistical consideration of the possible rotational isomeric states (RIS) for the chain. This is one of the adaptations of the Ising Model in polymers. (A second adaptation is the Flory-Huggins description of the free energy of mixing). The following discussion follows partly the presentation of Strobl in Section 2.4 page 53 of the text.

What is the Ising Model?

The Ising model consists of an array of particles that interact. The interaction leads to a change in state (spin for instance). For the simplest case only nearest neighbor interactions are considered. In application to the local structure of a chain molecule we consider a one-dimensional Ising model since the chain is a linear structure. The total energy for a chain can be calculated from a sum of interaction energies for each pair of chain units.

where is the interaction energy between a pair of chain units in the state .

Consider a polymer chain where the energy of one chain unit depends on the rotational isomeric state of all of the N units in the chain so the chain's energy is not simply N <u> but is given by considering all of the states of the chain and how these modify the local bond rotation. The relative populations of isomeric states for a chain will directly govern the chain flexibility and the persistence length and it is possible to consider the nearest neighbor interactions and to propagate these to the whole chain. This is done by calculating the partition function, Z, for the chain,

where is the group of all conformational states for the chain, i.e. for pentane there are 9 states, trans-gauche⁺, trans-gauche^-, t-t, g⁺-g⁺, g⁺-g^-, g⁺-t, g^--g⁺, g^--g^-, g^--t. u is the internal energy for the entire linear structure which for pentane involves 4 bonds, so four exponentials multiplied by each other. Knowing the partition function the free energy for the chain can be calculated,

f_p = -kT lnZ.

The internal energy per chain is,

e_p = f_p - Ts_p = f_p + T

For a polymer chain of length N the pentane calculation becomes bulky, there are N-1 summation signs, over the 9 states for polyethylene for instance, and each involves multiplying N-1 exponentials,

(the P symbol is similar to a summation but the terms are multiplied). t is called a statistical weight for a given pair of states. Since this calculation is unmanageable in a linear form for a chain of reasonable length, matrix math is used to calculate Z. For polyethylene, similar to pentane, there are 9 paired states listed above. The lowest energy state is the t-t state, planar zig-zag. For this ground state u = 0 and t_i1 = 1. Formation of a gauche+ state for the second bond from t-t requires an energy w₀ and,

The least favorable arrangement is g^--g⁺ or g⁺-g^- which creates a hairpin curve in pentane and has high steric interference which has an energy w₁w₀. The result of these considerations is that,

where

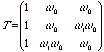
and the subscript 11 refers to the 11 component of the N-2 power of T. To reasonably solve for this component, T should be diagonalized by solving the homogeneous linear equations,

which leads to three eigenvalues, l₁, l₂ and l₃. Following Strobl (page 56), the solution for Z is given by,

and

and

Results from such calculations are very good for calculation of the entropy of fusion for a wide range of polymers, polyethylene: observed 9.9 J/(K mole); calculated using RIS 8.25 J/(K mole). Since there is no consideration of the volume expansion on melting, the enthalpy of fusion is lower than that observed experimentally, polyethylene: observed 4.10 kJ/mole; calculated using RIS 2.28 kJ/mole.

The fraction of isomer combinations and the fraction of each isomer can be calculated directly. This combined with bond angles and bond lengths can be used to calculate C_∞, the high-q structure factor, and using the Kratky-Porod model, the persistence length of a polymer. A value for C_∞ of 6.7 for polyethylene is observed experimentally and is calculated exactly from RISM. The figure below from Strobl's book that cites the original source Gawrisch, Brereton, E. W. Fischer, Polymer Bulletin, 4:687, 1981, shows how exactly the high-q structure factor can be calculated using RISM. Flory published a number of such calculations during his tenure at Stanford for most polymers existing at that time.

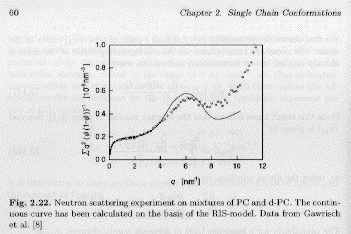
The Porod-Kratky Chain:

RISM can be used to calculate the persistence length, l_p, or the Kuhn step length, l_K = 2l_p, both of which can be experimentally measured, l_p by SANS and l_K in rheology measurements. In order to calculate l_p, for instance, a statistical definition of chain persistence is needed and this was a topic of interest for several of the seminal workers in Polymer Science, Kuhn in the 1930-40's, and Porod and Kratky as well as Benoit and Doty in the 1950-70's. There is current interest in chain persistence in a number of fields related to polymers such as in study of worm-like micelles, sol-gel derived nano-scale ceramic chains or zirconia for instance, and in polyelectrolytes. Flory gives an account of chain persistence in Appendix G (page 401) of his second book, Statistical Mechanics of Chain Molecules, that is fairly concise and is summarized here.

Porod defined persistence for a chain of continuous curvature, that is a chain where the individual bonds and bond rotations of RISM are blurred so that the chain can be considered to follow a self-avoiding walk. This is called the worm-like chain. For a chain composed of steps of length l' with an average angle between steps of q' and with k chain steps (different symbols are used since these may or may not be chemical bond steps) the average projection of the k'th bond on the first bond is l'a^k-1 where a = cos q'. a can be a fixed value of we consider chemical bonds with fixed bond angles in a freely rotating chain, i.e. a chain that does not consider rotational isomeric states. If we consider RISM then persistence would generally be higher, raising the value of a. The average sum of projections on the first bond (or on any bond in the chain) is the persistence length, a or l_p, of the chain which is generally larger than l',

where the latter equality is good for a large number of steps. The persistence length is related to C_∞ by (Flory page 111),

For polyethylene C_∞ is 6.7 and the C-C bond is about 1.5Å so l_p is about 5.8Å which is close to the experimental values observed from SANS and rheology, l_K. l_K seems to be the best value to use for consideration of the properties of a persistent chain, i.e. the rod length.

The persistence length can also be related to the extended chain length, L. L is not equal to nl since the chain units in RISM have valance angles.

Flory gives the following two expressions for the persistence length, a, for two cases, short chains (relative to a) or stiff chains,

and long chains (relative to a) or flexible chains,

Note that chain flexibility is always relative to the persistence length making this a central value for consideration of polymer behavior. Additionally, the number of chain units, N, in a chain is strictly based on the persistence unit or Kuhn unit of the chain for statistical calculations such as calculation of the entropy of the chain since the Kuhn unit is the physical basis for the chain step (not the chemical monomer unit or the statistical segment length). Generally it is considered that the persistence length does not have significant dependencies on temperature or composition but this is clearly not true for polyelectrolytes or for worm-like micelles and may be in error for hydrogen-bonding systems.