Rubber Elasticity

(Indented text follows Strobl, other follows Doi)

Elasticity of A Single Chain:

The spring constant associated with a single polymer chain is of importance in a wide range of situations from the development of a simple description of rubber elasticity to understanding flow behavior and other physical deformations of the chain. The basis of rubber elasticity is the Gaussian chain and most descriptions are limited by this framework. Despite this limitation the description of the elasticity of a polymer chain is one of the major success stories of polymer science. Elasticity in polymers is based on thermal motion of the chain units. Consider a jump rope that is being swung. The ends of the rope are pulled inward due to the kinetic energy of the rope. Similarly, the thermal kinetic energy of a polymer chain tends to oppose stresses applied to the random coil. Put differently, the chain seeks to maintain a random state and any force applied to deform the chain acts to reduce the randomness of the chain. This can be a compressive, tensile or shear force.

For a chain of length N and W0(r) conformational states the free energy can be written as a sum of the entropic and enthalpic contributions,

A = -kT ln W0(r) + C = 3kT r2/(2Nlp2) + C

where C is a constant associated with the enthalpy of the chain. The free energy is a function of the chain extension, r. Changes in this free energy with respect to r result in a force, -f,

f = -dA/dr = -3kT r/(Nlp2)

Thermal motion of the chain is the source of this force just as thermal motion of atoms in a gas give rise to pressure. Generally, we can speak of a spring constant f = K r, where K = 3kT/(Nlp2), for an ideal chain.

For an ideal chain the free energy associated with deformation in the "y"-direction comes solely from entropy changes.

Force = df/dy = -T ds/dy

The entropy is given by the partition function Z from s = k lnZ(y), where Z is the number of conformations available to the chain when the two ends are separated by a distance "y". The Gaussian distribution describes the probability of a given end to end distance,

p(x, y, z) = (2pR02/3)-3/2 exp{-3(x2+y2+z2)/(2R02)}

This reflects the number of conformations for a given end to end distance. For x = 0, z = 0 and y having a value,

Z(y) ~exp(-3y2/(2R02))

and the entropy is

s(y) = K + k(-3y2/(2R02))

Then the force associated with deformation of a single chain is force = 3kT/(R02) y

Free Energy of a Network (Rubber):

Consider a bulk sample of rubber composed of tens of millions of single chains connected by crosslink sites. For such systems it is appropriate to consider a continuum view and define a deformation by the displacement of a material element at position R in the unstressed state to a position R' in the stressed state. The deformation gradient tensor, Eij, describes the defomation in terms of a tensor expression Eij = dR'i/dRj, where i and j are any combination of Cartesian coordinates 1,2,3. Then Eij is a 3x3 matrix describing the relative positions of material elements on deformation.

As noted above, the free energy of a chain between crosslinks of N units with end to end vector r is

f = (3kT/(2Nlp2))r2

In the network chains of variable end to end distance exist so the free energy, A, must be integrated over r. If the rubber contains nc chains, and the probability of a chain of molecular weight N and end to end distance r is Y(N, r) then,

where K is a constant. This expression is simplified by the following assumptions:

1) The chains are Gaussian in the deformed and undeformed states.

2) Deformation is affine so r' = E • r where E is the deformation gradient tensor. Then the free energy for the deformed state is,

Integrating leads to,

Deformation of a Real Rubber:

Under isothermal conditions the change in free energy, dA, due to an infinitesimal strain, de, is,

dA = Vsab deab

The infinitesimal change in the deformation gradient tensor, dEab, is given by,

dEab = S deam dEmb

and the change in volume, dV, is,

dV = S V demm

where the summations are over the indicies m. From the expression for the free energy,

dA = SSS {nckT deam Emb Eab + (dK/dV)T V demm}

where the summations are over a, b and m. From this an expression for the stress, sab can be obtained,

sab = S(nc/V) kT Eam Ebm - Pdab

where the summation is over m.

Finger Tensor:

The deformation gradient, Eij = dR'i/dRj, relates the position in the stressed (prime) to the unstressed state. The Finger tensor is expressed by,

Bij = SEim Ejm = S dR'i/dRm dR'j/dRm

where the summation is over the index m. The Finger tensor describes the deformation in the absence of rotations and translations that do not lead to a change in the material position R relative to a coordinate system based in the material, i.e. a codeformational coordinate system. This tensor is necessary since the Flory expression for rubber elasticity does not consider translation and rotation as leading to a change in free energy. Then we can write,

sab = (nc/V) kT Bab - Pdab

The Cauchy tensor, Cij, is related to the Finger tensor by,

Cij = 1/Bij

The Eulerian strain tensor, eij (the strain for linear response), is related to these tensors by,

2eij = dij - Cij

Shear Deformation:

For simple shear deformation,

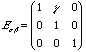
and Bij is given by,

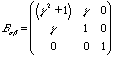
so,

sxy = (nc/V) kT g

sxx = (nc/V) kT (1+g2) - P

syy = szz = (nc/V) kT - P

The shear modulus is given by,

where nc is the number density of network chains.

Uniaxial Extension:

For uniaxial extension,

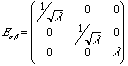
and Bij is given by,

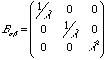
so,

sxy = (nc/V) kT g

szz = nc kTl2 - P

sxx = syy = nc kT/l - P

for sxx = syy = 0, P = nc kT/l, and

szz = nc kT(l2 - 1/l)