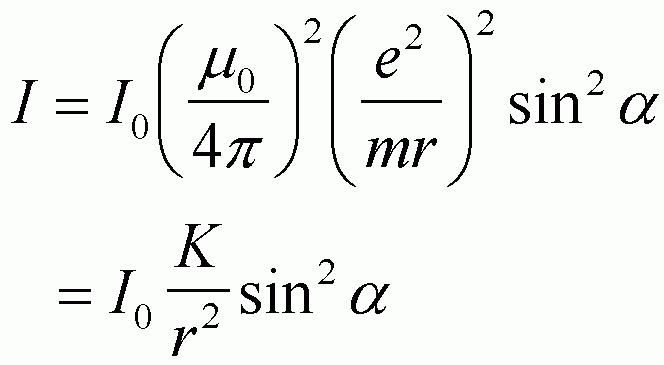
Class Notes: Chapter 4
Development of a Model for Diffracted Intensity
The diffraction pattern from a crystalline samples contains 2 pieces of information for each
Bragg peak.
1) the angular position of the diffraction line and
2) the intensity of that line.
So far we have dealt only with the angular position and it's description with Bragg's Law.
Chapter 4 deals with the calculation of the intensity of a diffracted beam. One reason that this is important is that for some diffraction peaks (as we saw in diamond cubic and FCC) the calculation of the diffracted intensity results in no intensity meaning that some of the lines predicted by Bragg's Law will not be observed in the pattern. The reason for this will become evident if we consider the calculation of the diffracted intensity. Also, since different peaks have different intensities, calculation of the intensity can yield additional information for indexing. Finally, the diffracted intensity is used to determine the composition.
The calculation of the intensity of a diffraction line involves a mathematical "building-up" of the crystal starting with electrons which are the source of the diffracted beam, atomic structure (atomic form factor), unit lattice site composition and finally crystal structure. The important information concerning positioning of electrons in a crystal involve PHASE INFORMATION, i.e. the relative positions and compositions in real space. For this reason, all calculations involve calculation of the Amplitude of the diffracted beam which is finally squared to yield the intensity in the last step.
X-rays are ionizing radiation. This means that the main effect of an x-ray on an atom is to remove electrons. Electrons which are removed from an atom are FREE ELECTRONS. All free electrons resonate in the same way so we can start the calculation of the intensity of a diffraction peak by considering the intensity of a single free electron. This intensity is called the Thompson factor as given in equation 4-1 on p. 125. The Thompson factor is angular dependent and depends on the state of polarization of the incident beam.
Diffraction occurs from tightly bound electrons (inner shell) if only elastic scattering is to be considered, i.e. nin = nout. Consider two Guitar strings, one tightly wound and the other loosely wound. A guitar string can be made to resonate by plucking. The frequency of this resonance will decay (inelastic) if it is loosely wound. Constant pitch relies on tight winding. Similarly, we might expect inelastic scattering from materials with many outer shell, loosely bound electrons such as Carbon. Since the wavelength is not maintained, interference effects are not observed. Inelastic scattering from loosely bound electrons are called Compton scattering in x-ray diffraction and incoherent scattering in neutron scattering. Compton scattering results in a basically flat background to the x-ray pattern for organic materials such as polymers which must be subtracted from the pattern.
The guitar string analogy is useful in considering the angular dependence of Compton scattering. Consider Bragg's Law, l = 2d sinq. This relationship indicates that lower angle correspond to lower wavelength or higher frequency. A high frequency guitar string is tightly wound and is not expected to display much decay in frequency. This means that we expect to see an increase in the Compton background as angle is increased and this is observed. That is, the Compton background is most important at high-angles and decays to 0 at low angles.
The Thompson equation describes the angular dependence of intensity scattered from a single, free electron. It is applicable to tightly bound electrons where elastic scattering can occur.
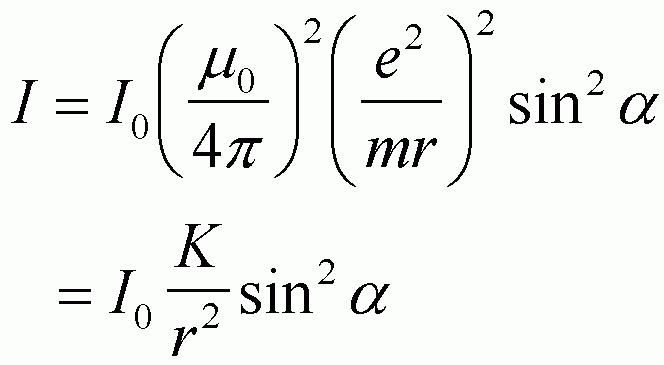
We have previously discussed the 1/r2 dependence of scattering. This results from any isotropic (same in all directions) radiation that is sampled using a fixed size detector since the amount of radiation per area decreases with the increasing area of a sphere surrounding the source. The angle a is the angle between the direction of acceleration of the electron (the electric field direction for the incident x-ray beam) and the direction of scattering.
The Thompson Equation can be used to calculate the effects of polarization on the scattered intensity. For plane polarized light and an experiment where an x-ray beam is incident on a single free electron, and the detector is in the plane of polarization of the beam, the angle, a, between the incident electric field vector and the direction of scatter is p/2-2q, so sin a = cos 2q. For this condition the Thompson equation yields a cos2 2q dependence for the sin2a term.
The orthogonal condition can also be considered, that is the detector is 90° from the electric field vector and doesn't depend on the scattering angle, 2q. This is shown in figure 4-3 on p. 125. Since a is 90° for all scattering angles and since sin p/2 = 1, the sin2a term in the Thompson equation is 1 for this arrangement.
An unpolarized incident beam can be considered to be made up of a sum of equal amplitudes of the two orthogonal components discussed above. The sum is made up of the sum of intensities divided by 2 to yield a normalized Lorentz-polarization factor for a single electron, (1+cos22q)/2 as equation 4-2 on p. 126. The figure below shows the behavior of this factor as a function of angle for unpolarized incident radiation.
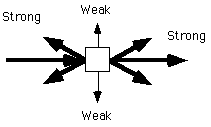
Depending on the incident beam's direction of polarization this behavior changes. For instance, in the Phillips diffractometer a monochromator just before the detector partially polarizes the x-rays perpendicular to the detector rotation angle. For this condition the polarization factor is close to constant, 1. Soller slits (polarizing slits) can also be inserted in the incident beam to strengthen this polarization effect (p. 195-197). In any case, careful consideration of the state of polarization is needed prior to calculation of diffracted intensity. Generally, the diffractometer is provided with a suggested equation for the calculation of diffracted intensity for different experimental geometries.
Phase of Scattered Beam:
Scattering from an electron can be considered to results from a series of steps. First a beam of x-rays has an electric field vector which oscillates at a given position with a sin wave. The electron is accelerated by this electric field vector so that the maximum acceleration occurs at the peak of the electric field sin wave and the least acceleration occurs where the electric field sin wave is zero.
The velocity of the electron is out of phase with this acceleration by 90°, reaching a peak where the original electric field of the incident beam is zero.
The change in momentum of the electron results in the emitted or scattered x-ray. This emission is 90° out of phase with the velocity of the electron. Summing the two 90° shifts yields a phase difference for the scattered x-ray of 180° from the incident beam or l/2!
This means that all of the scattered x-rays could destructively interfere with the incident x-rays if their directions coincided. Their directions only coincide in the direction of the incident beam so this effect is of no consequence. Since all scattered waves have the same phase and same phase shift from the incident wave we consider that their phase is identical to that of the incident beam for all practical calculations.
Atomic Scattering Factor:
To an x-ray, which interacts only with electrons, an atom is a collection of Z (atomic number) electrons. Therefore we might consider that the atomic scattering factor would be Z times the Lorentz polarization factor and the constants of equation 4-2. This is in fact the case for low-angles as in figure 4-6. The Atomic Scattering Factor is defined as the Amplitude scattered by a single atom divided by the Amplitude scattered by a single free electron and at low angle it is equal to Z.
At higher angle (smaller sizes) the internal arrangement of the electrons in an atom becomes important. For some arrangements the waves scattered from different electrons can interfere destructively leading to a decay in the overall intensity. This can only be calculated for fairly simple atoms and in general is a measured function of scattering angle deduced from perfect crystal diffraction patterns.
Figure 4-6 shows the general trend for atomic scattering factors which are tabulated in Appendix 10 pp. 648. Values in this table can be extrapolated to intermediate angular values with good accuracy. Continuous functions for atomic scattering factors are also available from the International Crystallographic Union via their web page if needed (LBL f, NIST f, IUCR f). Usually, appendix 10 is sufficient.
The square of the atomic scattering factor is identical to the scattering from an ideal gas because the definition of the atomic scattering factor, f, is basically the definition of an ideal gas composed of the atom of interest, i.e. scattering from a single, non-interacting atom, in a dilute condition.
Unit Cell Scattering:
We have begun to build up a model for diffraction from crystals. This begins with equations for a single, free electron, a single free atom and now progresses to placing these atoms in a unit cell where interference between different unit cell positions (all of which are scattering as if they were isolated atoms). We will consider waves emanating from the various unit cell positions and sum their amplitudes, and square this sum to obtain the diffracted intensity.
The sum of amplitudes involves consideration of the phase of the waves which emanate from each lattice position relative to the [000] position. We will want to determine general equations which describe the phase of a wave which emanates from different lattice positions as a function of the position. Then the amplitudes as a function of phase angle can be summed to describe interference.
Waves scattered from an atom at the origin, [000], is the base unit from which the phase differences will be calculated.
Diffracted intensity from (h00) planes.
The path difference for waves scattered from [000] and those scattered from (h00) planes is defined by Bragg's law as d = 2dh00 sinqh00 = l. dh00 = a/h where a is the unit cell parameter (x distance). For waves scattered in the qh00 direction the phase difference, f, is 2p which can be written in a more general way as: f = 2p (d/l), that is the path difference between two atoms, d, is proportional to the phase difference. The phase difference,
f, is an angle reflecting the amount you shift the sin wave for two waves when summing amplitudes. If the phase difference is 2p then the amplitudes just sum. If the phase difference is less than 2p then there is some amount of destructive interference which leads to zero intensity when the phase difference is p, i.e. 180° out of phase.
Consider an atom at an arbitrary translation in the x-direction from [000] of value "x" and a diffraction angle qh00. For this Bragg angle the path difference is l for an atom at position a/h. The path difference at position x between waves at qh00 from [000] and [x00] is d = (x/(a/h))(l) (by comparison of similar triangles in figure 4-8) or the fraction of l associated with the ratio of x to a/h. (That is, for an atom at a/h the path difference is l.)
The phase difference for this atom at [x00] and the [000] atom at qh00, is f = 2ph (x/a).
Usually we express the position of an atom by it's fractional coordinate, u = x/a, so this phase difference becomes: f = 2phu. (more generally, f = 2p(hu + kv +lw). The phase difference is a dot product between a real space position vector r of the atom, and the reciprocal space vector associated with the diffraction angle q = 4p/l sin q, f = q.r.
(You should notice immediately the similarity between this definition of the phase difference and the von Laue definition of the Bragg condition.)
Next this phase information must be included in the definition of the amplitude so that amplitudes from two atoms can be summed. In order to do this we need to review summation of amplitudes in complex space. p. 134.
Inverse Space View of Phase Differences from An Atom at [000] and one at [uvw] for an (hkl) reflection:
The real space location of an atom is given by the vector v = u a1 + va2 + wa3, and a set of planes in inverse space is defined by the vector H = hb1 + kb2 + lb3. The dot product of these two vectors corresponds to the projection of v in the direction H,
![]() as shown below:
as shown below:
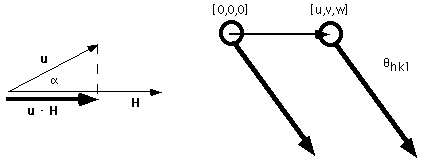
The dot product of u and H gives the projection of the atom translation in the direction of diffraction which is equivalent to the relative path difference (with respect to the wavelength). This means that the phase difference is simply f = 2p(hu + kv +lw), or the dot product of the two vectors in real and imaginary space time 2p.
Summing Waves of Different Phase:
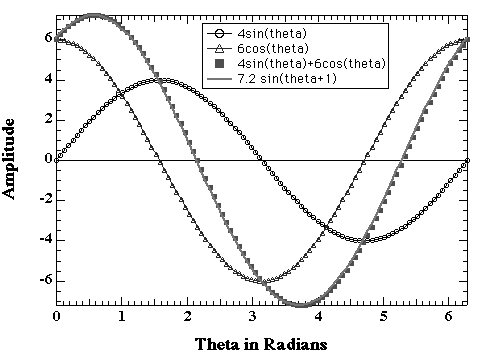
Open circles are a sine wave of amplitude 4 and open triangles are a cosine wave of amplitude 6. The sum of these two out of phase waves is a sine wave of amplitude √(42+62) and phase shift of 1 radian which is tan-1(6/4). This summation of two out of phase waves can be graphically visualized by an x-y plot in complex space where the x-axis is a cosine wave, taken to be in-phase with the first wave, the y-axis is a complex (out of phase with original wave or a sine wave).
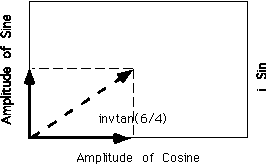
Figure 4-11 on p. 134 shows this for arbitrary phase waves.
Using this graphical view in complex space any wave can be written in terms of the phase angle with respect to a base cosine wave whose phase shift is 0:
Aeif = Acosf + iA sinf
Summation of two waves of different phase amounts to summation of the real and imaginary components which results in a wave of different phase and amplitude by the vector summation in complex space.
For an x-ray scattered from an atom we have already seen that the phase,
f, is given by:f
= 2p(hu + kv + lw)So we can write the amplitude and phase as
Aei2
p(hu + kv + lw)The intensity is the square of this complex number which is the imaginary number times it's complex conjugate (make the exponential power negative),
I = A2 ei2p(hu + kv + lw) e-i2p(hu + kv + lw)=A2
(Acosf + iA sinf)( Acosf - iA sinf) = A2 (sin2 f + cos2 f) = A2
Structure Factor for a Unit Cell, F(hkl):
The structure factor for a unit cell from a given set of (hkl) planes is calculated from the summation of the amplitude function from each atom in the unit cell [uvw]:
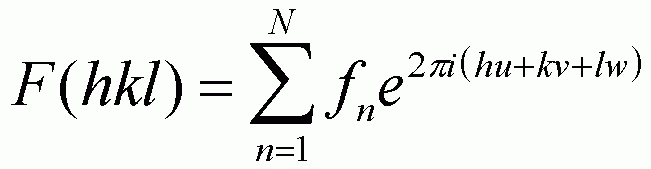
F reflects the amplitude of a wave scattered from the unit cell divided by the amplitude for a single electron. This definition is parallel to the definition of the atomic scattering factor, f, above.
Notice that the phase angle is 2
p times the dot product of the reciprocal space vector, (hkl) and the real space vector [uvw].Complex Exponential Relationships of Vital Use:
Since the calculation of the structure factor for a unit cell will involve manipulation of complex exponentials it is useful to give some relationships which can simplify calculations. These are listed on pp. 121 in section 4-5 and should be memorized.
Rule 1: e
npi = -1 if n is odd or 1 if n is even, i.e. = (-1)nRule 2: enpi = e-npi when n is an integer
Rule 3: eix + e-ix = 2 cos x
Calculation of Some Unit Cell Structure Factors:
a) Cell with one atom at (000),
F(hkl) = f
F2 = f2
e.g. simple cubic
b) BaseCC cell
2 atoms (0,0,0), (1/2,1/2,0)
F= f + fe2pi(h/2+k/2)
= f [1+epi(h+k)]
(h+k) is always integral so the result depends on if h and k are the same in terms of odd or even (unmixed) or different in terms of odd and even (mixed) by Rule 1 above:
Mixed hk => F = 0
Unmixed hk => F = 2f and F2 = 4f2
This means that many reflections will be missing from the BaseCC pattern compared to the simple cubic pattern. These missing reflections are a finger print of the BaseCC structure!
c) BodyCC
2 atoms (0,0,0) and (1/2,1/2,1/2)
Similar to BodyCC except that the rules go by (h+k+l) being even or odd:
(h+k+l) odd => F = 0
(h+k+l) even => F = 2f and F2 = 4f2
BaseCC has an (001) reflection while BodyCC doesn't
d) FCC
4 atoms (0,0,0); (1/2,1/2,0); (1/2,0,1/2); (0,1/2,1/2)
F = f[1+ epi(h+k)+ epi(h+l)+ epi(k+l)]
for Unmixed hkl => F = 4f and F2 = 16f2
for Mixed hkl => F = 0
i.e. no (100) reflections but will have (111), (200) etc.
Table 4-1 on p. 140 summarizes these conditions.
Structure Factor, F, for unit cells with different kinds of atoms:
e) NaCl is an FCC structure with Cl's located at the [0,0,1/2] edge positions. Both Na and Cl alone form an FCC structure so the unit cell has 4 atoms of each or a total of 8 atoms:
Na 000 1/2 1/2 0 1/2 0 1/2 0 1/2 1/2
Cl 1/2 1/2 1/2 0 0 1/2 0 1/2 0 1/2 0 0
The structure factor for this unit cell contains 8 terms:
F = fNa[1+ epi(h+k)+ epi(h+l)+ epi(k+l)]
+fCl[epi(h+k+l)+ epi(l)+ epi(k)+ epi(h)]]
Since both Na and Cl can form an FCC structure independently, you might expect that this common FCC structure factor, [1+ epi(h+k)+ epi(h+l)+ epi(k+l)] could be "factored-out" leaving the translation of the Cl lattice relative to the Na lattice. This is what is done:
F = [1+ epi(h+k)+ epi(h+l)+ epi(k+l)] [fNa + fCl [epi(h+k+l)]]
FCC Na and Cl with Translation
Thus, the FCC NaCl unit cell shows FCC rules modified for two atoms at a lattice site:
MIXED INDICES F = 0 (FCC rule)
UNMIXED INDICIES
(h + k + l) even F = 4(fNa + fCl)
(h + k + l) odd F = 4(fNa - fCl)
More complicated unit cells:
f) Hexagonal Closest Packed:
2 atoms at [0,0,0] and [1/3, 2/3,1/2]
F = f[1 + e2pig]
where g = [(h + 2k)/3 + l/2]
g can have fractional values so the value of F is complex!
Need to calculate |F|2 using the complex conjugate:
|F|2 = f2 (1 + e2pig) (1 + e-2pig) = f2 (2 + e2pig + e-2pig)
eix + e-ix = 2 cos x [From our previous complex number rules, Rule 3], so,
|F|2 = f2 (2 + 2 cos (2pg))
From Trigonometry rules, cos(2x) = 2cos2(x) -1, so,
|F|2 = f2 (2 + 2(2cos2(pg)-1))
= f2 (4cos2(pg))
where g = [(h + 2k)/3 + l/2]
This is 0 when (h + 2k) is a multiple of 3 and l is odd.
Results for Hexagonal are tabulated on p. 144.
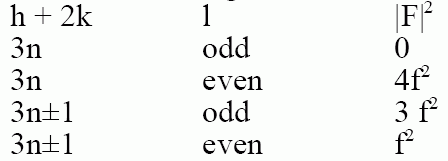
Intensity Calculations for Different Camera's
The diffracted intensity can be calculated from a series of terms related to:
1) which hkl reflection is being observed,
2) what wavelength is being used,
3) the unit cell parameters,
4) lattice type,
5) the number of planes in a unit cell contributing to each hkl reflection for a given unit cell, p (the multiplicity factor),
6) the geometry of the experiment,
7) intensity reduction due to thermal effects.
We have defined the first 4 of these parameters in terms of the polarization factor (1 + cos22q)/2 for unpolarized radiation, the Thompson Factor (K/r2) for scattering from a single electron and the unit cell structure factor |F|2 which depends on the atomic scattering factor f2, and the specifics of 1 to 4.
Ihkl = (K/r2) (1 + cos22q) |Fhkl|2 phkl (q-dependent from item 6) (q-dependent from item 7)
Multiplicity Factor, phkl:
For a simple cubic system there are 6 faces which contribute to reflections of the type {100} (counting positive and negative indicies), p100 = 6, there are 8 planes of the type {111}, p111 = 8. This means that the number of atoms contributing to a {100} reflection will be 6/8 times the number contributing to a {111} reflection, so the intensity of {100} will be 3/4 that of {111} just due to multiplicity. Notice that the number of objects contribution to the intensity is not squared since the intensity directly reflects the number of diffracting objects. (This is an important in phase analysis, i.e. the intensity is proportional to how much. This is also a useful way to define what the intensity means, i.e.
intensity is related to how much (how many atoms) at some size scale 2p/q.) Such multiplicity considerations have been worked out for all unit cells and is listed in Appendix 11
p. 651. Notice that the value for phkl relies on the assumption that all planes have equal probability of being oriented for diffraction to occur, i.e. this is really for a powder sample or a multi-grain sample. Orientation could have effects on multiplicity!
Geometry of Sample/Camera (Lorentz Factor):
The geometric arrangement of the sample with respect to the incident and diffracted beams leads to angular dependent terms. For the Debye-Scherrer Camera with a powder sample this function is:
![]() Debye-Scherrer (Powder Sample)
Debye-Scherrer (Powder Sample)
and for the rotating crystal method it is:
![]() Rotating crystal method
Rotating crystal method
These functions can be derived by a consideration of the geometry of diffraction for a diffraction peak of maximum intensity Imax and breadth B. The Lorentz factor accounts for the integrated intensity which is proportional to the maximum intensity times the breadth, B. B is a function of angle as we saw with the Scherrer approach to crystal thickness, B = 0.9 l/ (t cos qB).
The Breadth of a peak is proportional to dhkl/a if we consider a normalization in terms of a of a fixed fractional deviation of d, i.e. d has a "deviation" of 5%" then Dq = B would have a width of l/(a sinq). This times the Scherrer functionality of 1/(cos q) yields 1/(sinq cosq) = 1/sin2q, the dependence of integrated intensity for the Rotating crystal method.
For the powder method, this function needs to be further modified. For a powder sample the crystalline planes are randomly oriented. Plane normals are evenly dispersed on a sphere surrounding the sample. Planes with normals pointing at 90° correspond with a diffraction angle of 0. Planes with normals pointing at 180° (directly back) correspond with q=90 or 2q = 180.
The condition of 0 diffraction angle corresponds with the largest area of the sphere surface (the circumference since the normal points at 90°) while that of 180=2q the smallest (a single point towards the incident beam). This geometry follows a cosq dependence. That is cosq is a measure of the number of randomly placed planes that are geometrically arranged to give rise to a diffraction peak at 2q. The Lorentz factor for the powder method becomes cosq/sin2q.
We must also consider that the film in a Debye-Scherrer camera or the detector in a diffractometer has a constant surface area per diffraction peak while the cone of reflection is much larger than this. This means that only a fraction of the cone of reflection is observed which leads to a 1/sin2q dependence to the observed intensity (minimum fraction of Debye Scherrer Ring is probed at 2q = 90). The Lorentz factor for the powder method then becomes:
LF = cosq/sin22q = 1/(4 sin2qcosq)
The latter equality being due to the trigonometric relationship: sin22q = 2 sinq cosq from the math handbook.
Usually, the Lorentz Factor and the polarization factor are combined for a given instrument to yield the Lorentz polarization factor. Note that the polarization factor depends on unpolarized radiation which is not the case for x-rays from a crystal monochromator or for synchrotron x-rays. Usually the instrument you are using has the proper Lorentz-Polarization factor listed in the manual which accounts for the state of polarization of the beam and the geometry of the camera.
Lorentz Factor by Irradiated Volume Method:
The Lorentz Factor can be directly obtained by considering a crystal as a box and considering the volume irradiated by a beam incident at the Bragg angle:
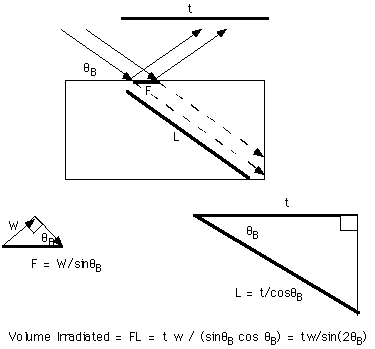
This yields the result for the rotating crystal method.
Absorption Factor:
The path length of the beam through the sample also depends on the sample geometry and the orientation of the camera with respect to this geometry. This leads to an angular dependent absorption which directly effects the diffracted intensity which is measured. For cylindrical samples in a Debye Scherrer camera this effect cancels with the Debye Temperature factor. For flat sheet samples this effect can be calculated and should be included in calculations of the intensity.
In a diffractometer such as the Phillips camera we used in the lab the sample rotates with the detector so that the angular dependence of absorption is mechanically removed from the experiment. This assumes that the sample is of infinite thickness. The thickness needed to satisfy this assumption can be calculated from t = 3.45 sinq/m.
The absorption follows thickness by the Beer-Lambert Law:
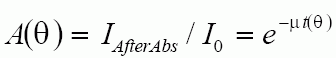
where m is the linear absorption coefficient and t(q) is the thickness of the sample as a function of angle. For a cylindrical sample, such as in a Debye-Scherrer Camera, the path length in the sample is the integration of a number of different A and B vectors as shown below.
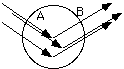
This can not be analytically solved for this sample shape and must be done numerically. The final answer is of a similar functionality to the temperature factor discussed below. Usually the temperature and absorption factors are considered to cancel in the intensity calculation for a Debye-Scherrer camera although tables of the absorption factor are available for more exact calculations. These tables need to be used if two intensities at widely spaced angles are to be compared (i.e. >20° 2q difference.)
For a Diffractometer sample, a flat plate sample which rotates with the detector, the x-ray path length is independent of angle. This can be shown by a calculation using the sample shown below and the incident angle, exiting angle, Bragg angle and beam diameter as variables. The calculation parallels that for the Lorentz Factor above except that the square below is a polycrystalline sample and the square above is a single crystal that might be within the polycrystalline sample below. Also, the sample below is rotated with the detector so that the incident and diffracted beams have the same angle, a = b. The two incident arrows indicate the extent of the incident beam and the foot print, F, on the polycrystalline sample equals the beam width, W, between these arrows divided by sina, F = W/sina, as shown above for the Lorentz factor. For shallow angles the foot print is big, for sharp angles the foot print is small.
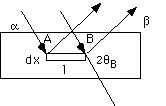
Here we are considering absorption and the beam will penetrate only to a certain depth in the sample, x. (This depth is fixed in the Lorentz factor since we are considering diffraction from a certain plane in a single crystal and the distances are extremely small (nm scale) where absorption is ignored.) Here x is a number on the order of millimeters. The change in the intensity which occurs on traveling a distance dx in the sample is given by the Beer-Lambert Law,
dI = (kI0/sina) e-2mx/sina dx
where the 2 in the exponential comes from the two equal path lengths to and from x (incident and exiting angles are the same in the diffractometer).
The total diffracted intensity is given by integration from x=0 to x=¥, where the integral of e-x is 1/x and the sina terms cancel so there is no angular dependence,
I = k/2m
This requires that the sample thickness is "infinite" at all angles. This thickness can be estimated by considering the ratio of the differential amount diffracted at x=0 and that diffracted at some depth t, dIx=0/dIx=t which is the ratio of the equation above,
dIx=0/dIx=t= e2
mx/sinaThe value for the infinite thickness approximation, t, depends on the lowest desired angle of diffraction and the desired ratio which can be taken to be 1000 for most situations.
Thermal Effects, Debye Temperature Factor:
Atoms move about their lattice positions due to thermal motion. This is the reason for thermal expansion and can explain heat capacity (these topics should have been covered in intro to mat sci and physics classes, a summary of this can be found in Kittel's book on Solid State Physics and you should definitely take a look at the Debye calculation of heat capacity if you are not familiar with this topic. It is also covered in most Physical Chemistry books such as Atkins and materials thermo books).
Atoms in a crystal display a mean free path,
s. This effects the intensity of the diffracted beam by a Debye-Waller Factor which is proportional to: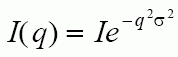
where q is 4
psinq/l. The mean free path of atoms at some temperature, T, can be calculated from the Debye characteristic temperature which is listed in appendix 13, p. 654.You should note that the functional form of the Debye-Waller Factor is a Gaussian Function which reflects a random distribution of atomic positions (bell-shaped curve function describing random distributions of large populations). The exponential form of the Debye-Waller factor cancels with the absorption factor for cylindrical samples, especially over small angular ranges, so can be usually ignored for wire or capillary samples run in the Debye-Scherrer camera. It should be included for diffractometer samples. Thermal broadening is pronounced in Al.
A different kind of thermal-like broadening is seen in polymer crystals which display high disorder of the first kind as discussed previously. This should display a similar angular dependence as the Debye thermal factor, so leads to a decay of the diffracted intensity with angle as shown in Figure 4-22, p. 157.
Thermal vibrations can also lead to an increase in background called Thermal Diffuse Scattering. Thermal diffuse scattering increases with angle in the same way that the diffracted intensity decreases with angle due to the Debye Thermal Factor.
The Temperature factor should be included for the diffractometer but doesn't' not need to be included for the Debye-Scherrer Camera due to partial cancellation between the absorption factor and the temperature factor for cylindrical samples.
Calculation of Intensities:
For the Debye Scherrer camera with cylindrical samples the diffracted intensity can be calculated from:
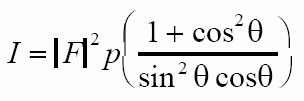
For a Diffractometer sample with a sheet sample which rotates with the detector the intensity can be calculated from:
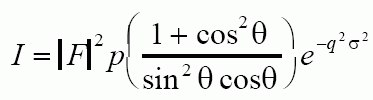
The calculation of relative intensity depends on the camera type. Usually, the relative intensity is converted to a normalized scale by dividing by the brightest peak intensity and multiplying by 10 or 100 to get the results on a percent of brightest peak scale for instance. Section 4-13 on p. 159 gives several examples of intensity calculation.
PROBLEMS WHICH CAN OCCUR:
The most common problem is preferred orientation of a sample. Since most XRD cameras sample only a circumference of the sphere of reflection, it is possible to obtain incorrect values for peak intensity. For this reason it is always useful to run a pinhole, transmission experiment using a flat film detector to determine if preferred orientation is present. This is the only way to assure yourself that there is no preferred orientation. Grinding a sample into a powder is a good way to approximate an unoriented sample but this can lead to disturbance of the structure in some cases.
Rotation of the sample is another possible solution. At this point you should have a clear understanding of why and how orientation can effect intensity measurements as this topic has been covered at length in the lab and lecture.
Extinction (Additional Absorption in Perfect Crystals, p.
512)
For a perfect crystal, the absorption coefficient can be enhanced at low angles for bright peaks due to two effects. First, each plane extracts some intensity for the diffracted beam. This loss due to diffraction at the Bragg Angle has not been considered (it is only important for very strong peaks). Second, Beams diffracted in the forward direction can under go a second diffraction event and be diffracted directly back into the incident beam. This secondary diffraction reduces the incident intensity and has the effect of reducing the diffracted intensity. This is also only important for perfect crystals and strong diffraction peaks.
For perfect crystals of calcite the absorption coefficient at the Bragg peak can be up to 70 times more than that off the Bragg peak (Klug and Alexander pp. 129).
Fine powders also show increased diffraction intensity since misaligned planes can contribute to the diffracted peak. Also, imperfections in the crystal lattice broaden the peaks and increase the integrated intensity as shown in figure 17-9 on p. 512.
As a rule of thumb, it is usually a good assumption that your sample is "ideally imperfect" which is the basis of the calculations above. When you work with perfect crystals and very strong peaks, Extinction should be considered in calculating relative intensity. The mechanics of considering extinction are beyond the scope of this course and you should refer to Klug and Alexander "X-ray Diffraction Procedures", 1967 for more details if needed.