Complex Exponential From Summation of Cosine and Sine Waves:

Complex Exponential From Summation of Cosine and Sine Waves:

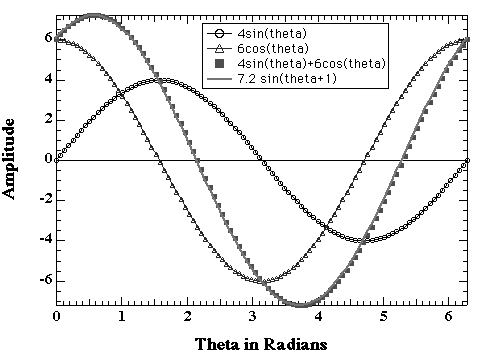
Any cosine wave with a phase shift of d can be described by the sum of a sine and a cosine wave of amplitudes A_s and A_c with no phase shift.

A cos(q + d) = A_c cos(q) + A_s sin(q)

This approach was used to plot A_s versus A_c and obtain the phase shift d.

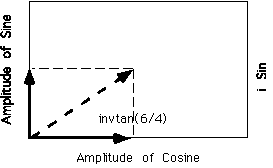
Figure 4-11 on pp. 118 shows this for arbitrary phase waves.

We can use the trigonometry identity,

cos(A + B) = cos(A) cos(B) - sin(A) sin(B)

To define A_c and A_s in terms of d and A:

A cos(q + d) = {A cos(d)} cos(q) + {-A sin(d)} sin(q)

So, A_c = {A cos(d)} and A_s = {-A sin(d)}.

This presents the problem that A_s is defined as a negative number, yet the amplitude of a wave is required to be a positive number. The issue is resolved by describing the sign of A_s as an imaginary number, i. Then the expression for the phase shifted wave can be written,

A (cos(d) + i sin(d)) = eⁱd

By expressing phase shifted waves in terms of eⁱd the mathematics for calculation of the diffracted intensity is greatly simplified since a number of simple math identities are available for the complex exponential.

Rule 1: eⁿpi = -1 if n is odd or 1 if n is even, i.e. = (-1)ⁿ

Rule 2: eⁿpi = e^-npi when n is an integer

Rule 3: e^ix + e^-ix = 2 cos x