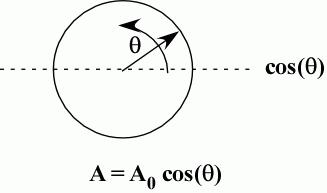
Figure 1. Cosine wave as a rotating vector.
Waves as Vectors:

Figure 1. Cosine wave as a rotating vector.
Figure 1 shows how a cosine wave can be depicted by a vector that rotates with a phase angle q. The cosine is the x-axis projection of this vector, cosine of the phase angle q times the vector magnitude A0. To sum two waves of different magnitude, B0 and A0 for instance, we consider two circles of different radii and sum the vectors using the parallelogram rule as shown in Figure 2.
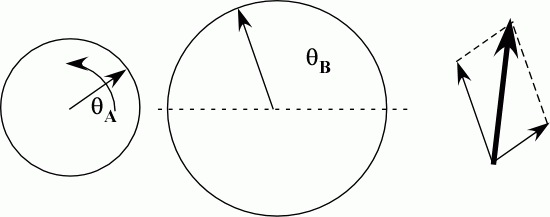
Figure 2. Sum waves as vectors
We could consider the vector representing a cosine wave as
composed of two parts, the x-axis or cosine part and the y-axis or sine part.
By summing these two parts the summed vector results.
x-part: Xsum = A cosqA +
B cosqB
y-part: Ysum = A sinqA +
B sinqB
An alternative to the geometric approach is to consider the x and y axes as arbitrarily existing in complex space. Complex space is a Cartesian coordinate system where the y-axis is a purely complex number and the x-axis is a purely real number. A complex number is a value times i where i = √(-1). An advantage of using complex space is that the wave vector can be represented in a simplier form,
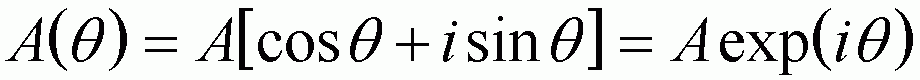
The sum of two waves, A and B is given by:
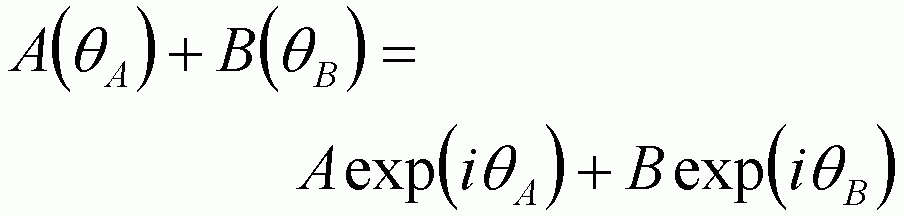
The advantage of complex space is when two vectors are multiplied which is a complicated problem without using complex numbers but is a trivial sum of powers using complex space:
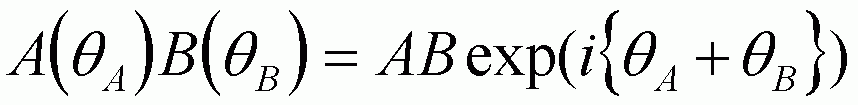
In calculation of the diffracted intensity we often need to consider multiplication of two waves so complex space is generally used to solve for the diffracted intensity. Three rules simplify the manipulation of complex exponentials:
Rule 1: enpi = (-1)n if n is an integer.
Rule 2: enpi = e-npi if n is an integer.
Rule 3: eix + e-ix = 2 cos x