X-Ray Diffraction Lab  Experiment 3
Wulff Nets and Pole Figures

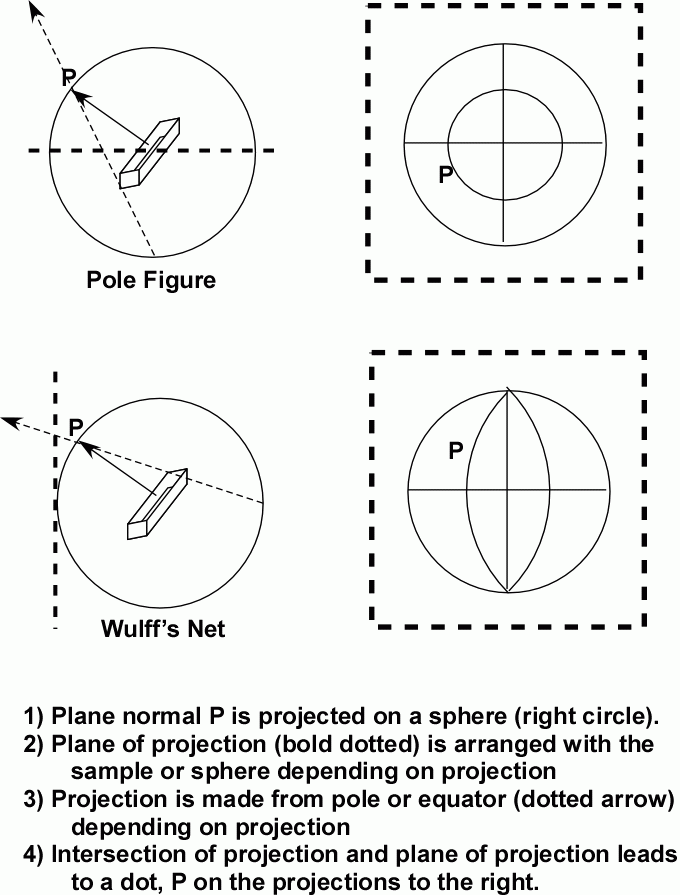
Wulff's nets and pole figures are two types of stereographic projections.  A stereographic projection gives information pertaining to the 3d structure and angles relating structural features in a two dimensional graphic.  For crystallography we are interested mainly in the orientation of crystallographic planes through their normals, and the angles between planes.  In most stereographic projections a sphere is considered that surrounds a crystal, for instance.  Normals to the crystallographic planes intersect the sphere at a pole, P, as shown below to the left for a pole figure (top) and a Wulff's net (bottom). 

The difference between a Wulff projection and a pole figure begins with the location of the plane of projection (dashed line in figure).  For a Wulff's net the plane is tangent to the sphere of projection at the equator and so is independent of the sample orientation while for the pole figure the plane of projection passes through the equator of the sphere of projection and lies generally along the main axes of the sample, i.e. the machine direction (MD) and the transverse direction (TD).  The reason for this difference is that the Wulff's net is intended to guide orientation of a single crystal with respect to the lab reference frame while the pole figure is intended to describe the orientation of crystallographic planes with respect to the samples reference frame.  For instance a Wulff's net might be used to align a single crystal for cleavage by identifying the (111) plane where the crystallographic and lab frames are important for cleavage, while a pole figure would be used to describe the distribution of (111) plane normals in a wire where the processing direction (sample coordinates) and crystallographic frames are important.

Projection of the sphere pole on to the stereographic projection is done differently for the two projects also, in the Wulff's net the projection is from the opposite equatorial position form the tangent location, while for the pole figure the projection is from the south pole to the pole on the sphere of projection.  The intersection of the projection line (dotted arrow in the figures) with the plane of projection is marked as a pole.  For the Wulff's net there will be a single pole for each crystallographic plane, while for the pole figure a distribution topo map for poles of different grains in a processed sample will result.  Then the pole figure is usually limited to a single set of planes while the Wulff's net shows many of the planes for the single crystal. 

A) Wulff Projection
Objective: To become familiar with Wulff net projections.

Background: (Old edition Cullity pp. 63-78 (Chapter 2).) (new edition p. 70-85 Wulff Nets and 402-431 Pole Figures)

Wulff nets are a type of stereographic projection which is typically used for single crystal samples such as silicon wafers in the microelectronics industry. They are also critical to electron diffraction in a transmission electron microscope (TEM) which will be the subject of a latter lab.

Figure 2.30 (new Cullity) shows the relationship between the plane normal of a crystal, a sphere of projection of this normal, and its depiction on a 2-d Wulff Net. A point on the equator of the sphere of projection is chosen as the point of projection for the Wulff Net with projection lines passing through the plane normals on the sphere of projection to the plane of projection which touches the sphere of projection on the equator. Because of the geometry of the Wulff projection, the Wulff net has the appearance of an equatorial mapping of the earth, i.e. a straight line through the equator passes through the projection at the center and arcs centered on the poles diverge at the top and bottom. The point of projection in relation to the crystal is decided by the geometry of a diffraction experiment. This will be discussed further in later labs. The purpose here is to manipulate stereographic projections in and of themselves but it should be kept in mind that rotations of these projections correspond to rotations of the sample in a diffraction experiment for identification of crystalline planes in a sample.

Wulff nets can be produced either manually or through the use of a computer program and you will become familiar with both approaches in this lab. Two programs are available, Desktop microscopist and Crystal 2.29. Shareware links to software for construction of Wulff Nets are linked on the main page.

On a sphere of projection a plane which passes through the center of the sphere intersects the sphere in a circle of maximum diameter on the sphere or a great circle. Planes which do not pass through the center of the sphere intersect the sphere in circles of smaller diameter than a great circle, a small circle. Lines of longitude (lines which connect NS) are great circles (meridians). Except at the equator, lines of latitude (EW) are small circles.

The angle between two planes is the same as the angle between the two great circles which are formed by their intersection with the sphere of projection or by the angle between the two normals to the planes, the two poles of the planes. The equatorial stereographic projection (Wulff net projection) of a great circle is an arc and the projection of a small circle is a circle as shown in figure 2-31 (new Cullity).

Poles, or plane normal projections on the sphere of projection become points on the Wulff's Net projection.

Angle between planes:
1) For two poles which lie on the same great circle (NS arc) the angle between the two poles (and their corresponding planes) can be measured directly off the Wulff's Net as shown in figure 2-33.

2) For two poles which do not lie on the same great circle the projection (or the Wulff's Net) must be rotated so that the two poles do lie on a great circle and then the angle between planes can be determined from the projection. This is equivalent to rotation of the sample in the diffractometer. This procedure is shown in Figure 2-34. This type of rotation parallels rotation of the sample in a diffraction experiment in a plane normal to the incident beam.

Standard Projections:
The plane of projection can be chosen to coincide with a standard low index plane (001) etc. for the crystal system of interest. This is termed a (001) standard projection for instance. For a standard projection the plane of projection will appear at the center of the Wulff net.

2) For a specific standard projection (e.g. 001 of figure 2-39 p. 82) the north, south, east and west edges of the Wulff Net correspond to orthogonal planes at their respective angles The position of a pole (hkl) can alternatively be determined by calculation of the angles between the plane of projection and the pole of interest using the standard formulas given in the back of Cullity (appendix 3) and the method of determining angles between planes give above.

Determining the great circle trace (intersection of a plane with the sphere of reflection) for a pole.
This procedure is shown in figure 2-35 on page 79.

Rotate Wulff's net so pole is on the equator. Then find trace by finding the longitude line (NS) which is 90° from the pole. Angle between traces can be determined as shown in figure 2-36 of Cullity on pp. 79.

Rotation of a pole about an axis.
1) Rotation about an axis normal to the projection can be done by rotation about the center of the Wulff's net the required number of degrees.
2) Rotation about an axis lying in the plane of the projection:
    a) Rotate the Wulff's Net so the axis falls on the NS line.
    b) Then move the poles along lines of latitude (EW) the required number of degrees.
This is shown in figure 2-37 on pp. 80 of Cullity. W to E is positive rotation angle. Cullity shows what to do if you reach the edge of the projection. (bottom right to top left etc.)
3) Rotation about an axis lying at some angle to the plane of projection (i.e. a pole about another pole):
    a) Bring the pole of the axis of rotation to the center of the projection by compound rotations of the type of 1 and 2 above.
    b) Rotate the required number of degrees using 1 above.
    c) Return the projection back to the original state by undoing "a".
This procedure is shown in figure 2-38 on pp. 81 of Cullity.

Part A of this lab will involve performing the problems given on the next pages. These should be done either manually or using the computer programs provided. Everyone should get a chance to become aquainted with the program for Wulff net construction and manipulation even if you decide to construct the nets manually.

B) Pole Figures
Objective: To become familiar with Pole Figures.

Background: Cullity pp. 402-431

Wulff's nets are one kind of stereographic projection which are useful mostly for single crystal samples or in the TEM where a single crystal in a polycrystalline sample can be isolated through the use of an extremely thin sample and a fine beam. Wulff's nets are used for single crystals used to produce computer chips (silicon or germanium diamond cubic systems) where the electrical properties and chemical properties (used in etching) vary greatly with crystalline lattice direction.

In many industrial circumstances samples are polycrystalline and are formed with a preferred axis of orientation of crystalline planes, i.e. in rolled sheet metal, metal fibers, and in virtually all polymer samples which have been industrially processed, blown films, fibers, extruded samples, cast sheets. In these cases the sample you are interested in has at least one direction related to the processing conditions. This direction is often called the machine direction (MD), or draw direction. If the sample is a fiber the MD is the only important direction since the crystalline orientation is usually considered random about the other two directions, i.e. a fiber is cylindrically symmetric.

For sheet samples there is a sheet normal direction (ND) and a cross direction (CD) which define an orthogonal coordinate system of importance to sample properties. This is true for most polymer applications and many metals applications.

Since such industrial samples differ dramatically from the single crystal samples natural to Wulff's net stereographic projections so it is not surprising that a stereographic projection native to these samples has been developed. The samples are polycrystalline so a separate stereographic plot is needed for each set of crystalline planes. Also, the crystals display a distribution of orientations so the plots will show regions of high probability of orientation rather than discrete directions of orientation. Pole figures are very useful to describe the mechanical and electrical properties of a typical industrially processed sample, i.e. the strength of a fiber in the draw direction or the strength and failure properties of a blown film in MD and CD.

Most stereographic projections are produced by computers so there are two features where you are likely to interact with these graphs. First is in setting up the parameters for a triple axis goniometer for creation of a pole figure (this is mostly beyond the scope of this lab but is described in Cullity on page 411). Second in interpretation of a pole figure produced by a computer as an aid in qualitative description of mechanical properties of a sample. This lab focuses on your becoming familiar with pole figures through several exercises and do not involve measurements, unfortunately. We will perform some crude experiments involving pole figures when we use the film camera in a later lab.

Concept of a pole-figure for a polycrystalline sample is fairly simple. A polycrystalline sample with preferred orientation is placed at the center of a sphere so that the MD lies in the equatorial plane of the sphere. Normals to one set of planes are projected on to the surface of the sphere, just as they are in the Wulff net projection. A plane is set in the MD/CD plane along the equator of the sphere and a line is connected from the south pole to the normals on the surface of the sphere. The pole figure looks like a dart board (concentric circles) since it is made by projecting the sphere of projection onto a plane from a polar perspective. Where these lines cross the plane of projection a spot is recorded.  Since pole figures represent only one plane they must be referred to by the plane which is considered, i.e. the (hkl) pole figure.

For a film or sheet material the preferred orientation is referred to by the preferred family of crystalline directions in the MD of the sample <uvw> and by the family of planes in the MD/CD plane of the sample {hkl}.

This lab is basically aimed at your becoming familiar with pole figures. It involves your conducting several exercises to demonstrate that you are familiar with these stereographic projections.
1) Problem 14.9  in the text. Use polar graph paper included in this lab.  (You will need figure 14.9, 14.10, and figure 14.12)
2) Polyethylene has an orthorhombic crystalline structure with 2 mer units per unit cell and lattice parameters a=7.40, b=4.93 and c =2.534Å. Why is the c dimension so much smaller and so much more specific in distance when compared with a and b directions?

The diffraction pattern from PE contains three prominent peaks corresponding to the (110), (200) and (020) planes. This lab includes two sets of pole figures for these planes. Determine the ideal orientations which correspond with these pole figures and qualitatively describe the preferred orientation in these two samples. Relate the chain direction to the film directions, (the chain axis is always the c-axis for polymer samples).