Simplified Road Map to Reciprocal Space:

Simplified Road Map to Reciprocal Space: Simplified Road Map to Reciprocal Space:

(What to do when you're lost in Reciprocal Space)

Rule 1: (Why am I here:) The diffraction image seen in a pinhole photograph or in a Debye-Scherrer photograph is an image of reciprocal space. You are here because you want a more direct way of sorting out what is going on in your measurement.

Rule 2: Which way is up? The reciprocal lattice is constructed from an arbitrary starting point in the lattice. The starting point can be fixed but it is arbitrary, i.e. H₀₀₀ doesn't correspond with the 000 position of the crystal.

Rule 3: Construction of a Road map for Reciprocal space. This just follows some simple rules.

To construct the reciprocal lattice use b₁ = a₂ x a₃/V and the like.

Rule 4: Conditions of Reciprocal lattice:

|b₁| = 1/d₀₀₁ and the like.

For a reciprocal space vector H_hkl = hb₁ + kb₂ + lb₃

The vector is perpendicular to the plane (hkl) and has a length |H_hkl| = 1/d_hkl.

Rule 5: Simple rules of life in reciprocal space. The projection of a real space lattice vector on its corresponding reciprocal space lattice vector, i.e. the dot product, is equal to 1. All other dot products of lattice vectors are equal to 0 for an orthogonal (right angle) lattice.

b₁^.a₁ = |b₁| |a₁| cos a = 1 because a is 0 and |b₁| = 1/d₀₀₁and |a₁| = d₀₀₁

b₁^.a₂ = |b₁| |a₂| cos a = 0 because a is 90°.

These two rules can be used to obtain the Laue equations (vector form of Bragg's law) and the equations for zone axis's we have been using.

Rule 6: The reciprocal lattice completely describes a crystal, just as a real space lattice completely describes a lattice. The two contain the same amount of information, the format has changed…

Reciprocal Lattice and Diffraction:

1'st deal with real space and get a reciprocal parameter.

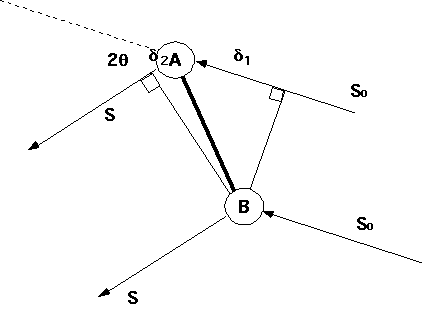
For 2 points A and B consider an incident unit vector wave of x-rays S₀ and a exiting x-ray of unit vector S. The path difference for point A relative to B for S₀ is d₁ = S₀ ^. AB. The path difference for point A relative to B for S is d₂ = -S ^. AB. The total path difference is d = d₁ + d₂ = -AB ^. (S - S₀). The phase difference is f = 2pd/l = -2p (S - S₀)/l ^. AB. For diffraction the phase difference, f, is equal to n2p so, for diffraction, (S - S₀)/l = 1/AB.

Figure. REAL SPACE view of Diffraction.

How Real Space picture relates to Reciprocal Space:

Now consider that (S - S₀)/l has reciprocal units, so is a vector in reciprocal space, (S - S₀)/l = hb₁ + kb₂ + lb₃. For totally constructive interference to occur, i.e. for diffraction to occur, the reciprocal space vector associated with the diffraction geometry, (S - S₀)/l must have the same direction as the vector normal to the AB plane and have a magnitude equal to 1/d_AB. That is the vector (S - S₀)/l must end on a reciprocal lattice point P_hkl.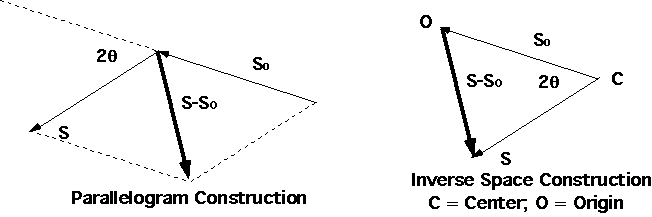

Figure. Relationship between Real Space and Inverse Space Constructions

The vector (S - S₀)/l can be obtained by a parallelogram construction as shown above. In construction of the inverse space vector the origin of the unit vectors S and S₀ are shifted so they coincide. This point is called the center of the experiment and labeled C. The origin of inverse space is the point where the incident unit vector ends. This point is labeled O and is taken as P₀₀₀. A construction showing the vector S-S₀ is shown above.

By swinging the vector S through the angle 2q the vector S-S₀ changes length and direction. In this process a sphere is created (a circle in a 2-d drawing) centered on the point C and with the point O on the sphere surface at 2q = 0. If an inverse lattice point falls on the surface of the sphere traced out by S-S₀ then a diffraction event occurs. The sphere is called the sphere of reflection for obvious reasons…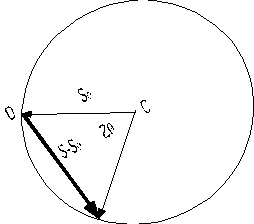

Figure. The Sphere of Reflection…For comparison with the inverse space lattice all "S"'s are divided by l.

For a fixed inverse space lattice and a fixed wavelength l it is unlikely that a inverse lattice point will fall on the sphere of reflection. The radius of the sphere of reflection is 1/l.

XRD Experiments in Inverse Space. (A new way to understand the XRD pattern)

Consider a powder pattern. The pattern results from many grains which have arbitrary orientation with respect to the incident beam. This can be simulated in inverse space in two ways,

A) By rotating the inverse lattice about the origin keeping the experimental directions fixed, i.e. keeping S and S₀ fixed.

B) By rotation the experimental directions about the origin, O, keeping the inverse lattice fixed.

The two methods are completely equivalent.

The Sphere of Reflection will trace out a new, larger sphere of radius 2/l when it is swung through all angles of incidence. This second sphere is called the limiting sphere. The inverse size associated with the limiting sphere is the maximum inverse vector that can be seen in the diffraction experiment, i.e. the inverse of the smallest size form the origin, l/2.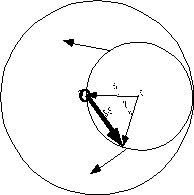

Figure. The Limiting Sphere

Since the sphere of reflection passes through the origin, the inverse of infinite size, there is no large limit to the size that can be observed in diffraction.

In a power pattern a single lattice point will trace out an arc on the surface of the sphere of reflection since the sphere of reflection can rotate about the origin.

Consider a Laue Experiment where l varies. Here the sphere of reflection is fixed in orientation with respect to the reciprocal lattice but the radius of the sphere of reflection increases and decreases to enhance the chance of intersecting a reciprocal lattice point. The lattice points will trace out an arc on the surface of the sphere of reflection as wavelength is changed.

Consider a Rotating crystal Experiment. Here the result is similar to a powder pattern but only one axis of the sphere of reflection is rotated. The figures in Cullity, in appendix 1 should be referred to (p. 480) to get a clearer idea of these three experiments.

Rotating Crystal, compare Fig. A1-9 p. 490 with Figure 3-10 p. 96

Powder compare figure A1-10 P. 491 with Figure 3-13 P. 99

Laue, compare figure A1-12 p. 493 with figure 3-6 p. 93.

Inverse Space and Momentum Change.

Inverse space has many uses. In addition to giving a qualitative impression of the source of a diffraction pattern, another major use is in relating the momentum change of the incident x-ray photon to the diffraction experiment. This is basically a particle view of diffraction. The momentum of a particle has direction, p = mv. In chapter 1 we noted that the momentum of a photon (x-ray particle) is given by p = hn/c =h/l (c/|c|). In diffraction we consider an elastic collision (elastic scattering) so the absolute value of momentum is constant. The change in momentum for a diffraction event is related to |p| times 2sinq as you can easily verify by basically the same sketch we used to derive Bragg's Law. For this reason, the vector (S - S₀)/l is often called the momentum change vector and inverse space is sometimes called momentum space. The vector q is used in some areas of diffraction, |q| = 4p/l sinq = 2p/d = |2p(S - S₀)/l|.