- State if the following
are true or false:
(a+b)+c=a+(b+c)
(a-b)=a+(-b) a*b=abcosq
(ma)*(nb)=mn(a*b)
a*(b+c)= (a*b)+(a*c)
if a┴b then a*b=0
axb*c=a*bxc
(ma)x(nb)=mn(axb) ax(bxc)≠(axb)xc
bxa=-(axb)
c=axb where c is ┴ to a and b
- Determine in rectangular
Cartesian form the unit vector which is parallel to the vector v=2i+3j-6k
where i, j, and k are unit vectors.
- Determine in rectangular
Cartesian form the unit vector which is along the line joining points
P(1,0,3) and Q(0,2,1).
- Show that if the vectors
a, b, and c are linearly dependent then a*bxc
= 0.
u = 3i + j - 2k
v = 4i j - k
w = i 2j + k
- Let the axes Ox1x2x3
and Ox1x2x3 represent two
rectangular Cartesian coordinate systems with a common origin at O, as
shown below:
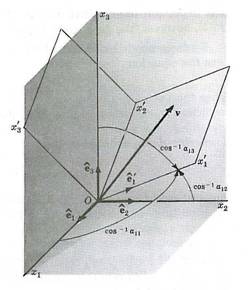
Derive an
expression to relate one set of coordinates to the second if the second set
of coordinates is merely the first set of coordinates rotated about the
origin.
![]()
