Introduction to Thermodynamics
![]()
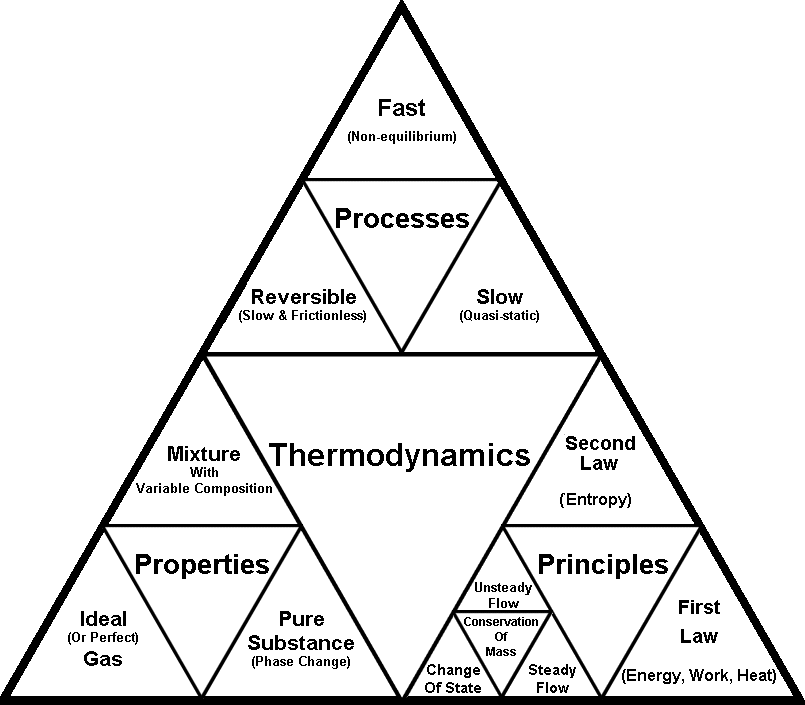
image: http://gaia.ecs.csus.edu/~reardonf/MET140/thermtri.htm
The subject of thermodynamics was born in 1883 when J. Willard Gibbs published his classical paper, “On the Equilibrium of Heterogeneous Substances.” In his work, Gibbs presented the science of thermodynamics and provided a formalism that is used to describe all phenomena that influences the condition of matter. In the simplest form, thermodynamics focuses on how matter is effected in way beyond kinetic and potential energy, namely mechanical work resulting from the expansion and contraction of materials, as well as the effects from heating and/or cooling a material. In this section, we will discuss several basic, but critical aspects of thermodynamics that must be utilized in modeling polymeric systems. To begin, we will review the laws of thermodynamics. Next, we will discuss how to define and classify thermodynamic systems and thermodynamic functions, variables and properties. Next, some general expressions for the laws of thermodynamics will be given that will serve as the building blocks for later derivations. Key terms, such as enthalpy and free energies, as well as experimental variables, such as the coefficient of thermal expansion and compressibility, will be defined. Maxwell relations will then be used to incorporate the experimental variables into expressions for thermodynamic parameters in terms of state variables of the system, in this case, temperature and pressure.
First Law:
There exists a property of the universe, called energy, which cannot change
no matter what processes occur in the universe. In other words, energy can
not be created, nor destroyed by any process…it is transformed from one for to
another (for example, entropy to enthalpy).
Second Law:
There exists a property of the universe, called entropy, which can only change in one direction no matter what processes occur in the universe. In other words, all process, if allowed to, will tend to a state of randomized disorder.
At this time, it would be good to give an example of how the first and second laws of thermodynamics interact. Say we take a new deck of playing cards directly out of the box. The cards are neatly stacked and arranged in the proper direction. At this “state”, the cards have the lowest entropy (highest order) possible. Now, the nicely stacked deck of cards are pushed off a table and scatter on the floor…we have a mess of randomized playing cards that are no longer stacked and oriented in the proper direction. To put the cards back into their original form, we would have to put work into the system to reduce the entropy (increase the order) until the cards are at the state with the lowest entropy (neatly stacked).
Zeroth Law (unusual numbering, I know…):
A universal absolute temperature scale exists and has a minimum value, defined to be absolute zero, and the entropy of all substances is the same at that temperature. Theoretically, zero degrees Kelvin or Rankin is the lowest temperature attainable (which can not be reached in reality). At this theoretical temperature, all molecular motion has stopped and all molecules have zero entropy.
In this section, we will classify the systems of which we want to study. It is important to define and classify a system for several reasons. First, it breaks the problem into manageable, solvable nodes that if necessary, can be combined to solve a larger, more complex problem. Second, this allows us to establish assumptions to simplify our models to make them mathematically manageable without providing significantly misguiding results. Finally, an intimate knowledge of the borders and limitations of the systems is critical for establishing realistic boundary conditions…a necessity for solving the typical differential equations often seen in mathematical models. In addition, one must also be aware of what materials make up the system, such as blends, phases, etc.
The first step in describing a system is to define what material or process if of interest. For example, does the system of study include all aspects of a process (reactors, distillation columns, etc.) or are we primarily interested in one component, say the reactor. Once the system of interest has been defined, they can be categorized using the following systems:
|
Unary vs. Multicomponent |
|
Unary are the simplest chemical system, since they are composed of only one component. Multicomponent systems increase in complexity with the further addition of components to the system. A glass of water can be defined as a unary system, while a glass of sugar water can be defined as a multicomponent system. |
|
Homogeneous systems contain only a single phase, such as an ice cube below 0 °C, where a heterogeneous system contains multiple phases, such as a glass of ice water (with cubes) at a uniform temperature of 0 °C |
|
A closed system makes no exchange of matter with its surroundings, such as closed bottle of water. An open system describes a system that exchanges matter with its surroundings, such as a glass of overflowing water under the tap. |
|
A nonreacting system does not have a chemical reaction occurring within its boundaries, with our previously mentioned reactor as an example |
|
Most of the systems we will study are considered otherwise simple. Complex systems arise when energy is exchanged by means other than thermal, mechanical, or chemical changes. Such instances include gravitational, electrical, magnetic, or surface influences. |
Functions, Variables, and Properties
The first term we will define is a state function, which depends only on the current condition of the system and not on how the system arrived at that condition. For example, the temperature of our glass of ice water is a state function, meaning that it doesn’t matter how it got to 0 °C (say through an infinite series of heating and cooling), only that the water is at that temperature. State functions are critical for solving thermodynamic problems because they only depend on the state of the system, and thus, the change in the values of a state function is simply the difference in values of two different points. This means the change in the state function is identical for every process that converts a system from its initial state to the final state…its value is independent of the path of which the system is converted from its initial to final state. This realization allows the engineer to address a complicated process (or path) by choosing the simplest means of proceeding from initial to final state.
The next item, the process variable, is a quantity that only has meaning for a changing system. The values of the process variables are thus, dependent on the path of which the process has proceeded. The two primary subcategories of process variables are the work done on the system (positive value) and the heat absorbed by the system (positive value). Work (w) is developed by a vectorial force acting upon a body (F) that results in a vectorial displacement (x), and is given by:
![]()
Upon integration for a finite process, the force relative to position (F(x)) is integrated over the finite x to give:
![]()
The above equation shows that work is only generated in a dynamic system, and thus cannot be associated with a static system…work is a state variable. Heat can be thought of in a similar fashion as work, in that it is always associated with a change in conditions of a system. It is meaningless to think of heat as a particular quantity (a heat content) for a static system, since flow and changing values are inherent aspects of the nature of heat.
Intensive properties of a system may be defined to have a value at a “point” in a system. Temperature (T), pressure (P), and concentration (c) are examples of intensive properties, since each point in a system (x, y, z, t) can have different values which can change with respect to time. To illustrate, we consider the earth’s atmosphere. As we move further away from the ground, the temperature and pressure of the air decrease as we proceed through the atmosphere.
Extensive properties are representative of a system as a whole, and do not vary from point to point within the system. The volume (V), number of moles (n), internal energy (U), and entropy (S) of a system are all examples of extensive properties.
It is often possible to derive intensive properties from extensive properties, typically by taking the limit of the ratio of two extensive properties. For example, the concentration in a system (c), can be defined as:
![]()
It is also worth noting that intensive properties can only depend on the values of other intensive properties. It does not make sense to try to define a property specific to a point in a system (the intensive property) with a property that is representative of the whole system (extensive property). In contrast, an extensive property can be expressed as the integral of the intensive property over the extent of the whole system.
Expressions for the Laws of Thermodynamics
As we stated in the first law of thermodynamics, energy is conserved in a process. This means the internal energy of any system (U) that undergoes a process is the sum of the transfer of energy across that system’s boundaries, and can be expressed by:
![]()
Where U is the internal energy, Q is the quantity of heat that flows into the system, W is the mechanical work done on the system by the external pressure exerted by the surroundings, and W’ is all other kinds of work done on the system during the process. To clarify the signs of Q, W, and W’, we note that if heat flows into the system, Q is positive and if work is done on the system by the surroundings, W and W’ are positive.
We know from the second law of thermodynamics that for every volume at every instant in time and for every process, entropy (S) is created. Of specific interest is the rate at which entropy is increasing (dS). The rate of increase for entropy is greatest for irreversible processes that occur rapidly at conditions far away from their state of equilibrium. One such example is the autoclave free radical polymerization reaction (which takes place at conditions near 2*10 Pa and 250 °C ) of ethylene to form low density polyethylene. The rate of increase of entropy is lowest (and approaches 0) in reversible processes for which each step is infinitesimally deviated from equilibrium. An example would be our stagnant glass of ice water we discussed earlier. On the surface of the ice cube, small amounts of energy is being transferred between the ice and the water, and thus the water with the glass, and finally the glass to the room, resulting in the eventual melting of the ice cube. During this process, the ice, water, and glass all periodically deviate slightly from the equilibrium temperature of 0 °C.
As stated before, entropy is a state function, meaning that the change in entropy is related to the heat absorbed by the system at each “step” of a reversible process, and can be expressed by:
![]()
Where T is the absolute temperature (Kelvin or Rankin scale) of the step.
The first two laws of thermodynamics can be combined to give the following:
![]()
Where the work term is expressed as:
![]()
and is negative because we are actually determining the work done by the system.
Definitions of Key Terms in Thermodynamics
The energy functions, namely the enthalpy (H), Helmholtz free energy (A), and Gibbs free energy (G), are measures of energy of a system that differ than the internal energy (U) that we discussed in the first law of thermodynamics. These functions can be used to simplify the description of a system in a form that is more convenient that discussing in terms of the internal energy.
The enthalpy (H), which is defined as:
![]()
Upon differentiation:
![]()
By substituting dU from the combined equation for the first two laws of thermodynamics, we obtain the alternative form:
![]()
The enthalpy term was originated to simplify the description of the heat engine taken through cycles. In this case, only mechanical work is done, meaning dW’=0, and the process occurs at atmospheric pressure, so dP=0. So, for an isobaric process (noted with the subscript “P”), we can relate the enthalpy to the entropy and thus, the heat transferred to a system by:
![]()
For this process (isobaric, reversible), we can measure the reversible heat exchanges of the engine with its surroundings.
The Helmholtz free energy (A) is a state function that can be represented by:
![]()
Upon differentiation:
![]()
By substituting dU from the combined equation for the first two laws of thermodynamics, we obtain the alternative form:
![]()
The Helmholtz free energy was devised to simplify the description of systems that undergo isothermal processes (noted with the subscript “T” representing conditions where dT=0), giving the following expression.
![]()
So, for an isothermal reversible process, the Helmholtz free energy can be used to report the total reversible work done by a system. Helmholtz free energy is often referred to as the “work function”
The Gibbs free energy (G) is similar to the Helmholtz free energy and is given by:
![]()
Upon differentiation:
![]()
The Gibbs free energy was introduced to be used in processes where the temperature and pressure are held constant (dP=0, dT=0). This simplifies the analysis of the process one step beyond the Helmholtz free energy, which only includes isothermal processes. So, for an isothermal, isobaric process:
![]()
The change in Gibbs free energy for an isothermal, isobaric system reports the total work done on the system other than mechanical work. This is critical for polymer scientists, since the Gibbs free energy characterizes process such as phase transitions and chemical reactions.
The attached figure shows the relationship between the various thermodynamic properties with respect to temperature. Note the changes in the functions at the transition temperature (in this case, the crystallization temperature noted as Tc). The set of images in column (a.) represent a first-order transition while the plots in column (b.) represent a second-order transition.
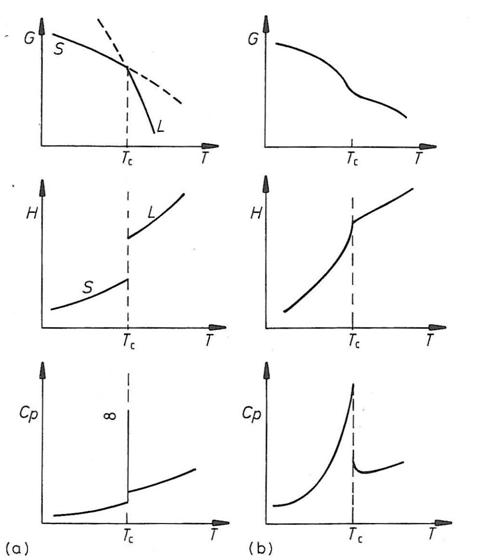
image: Gaskell, D. R., Introduction to the Thermodynamics of Materials, 4th edition, Taylor and Francis Group, 2003.
At this point, it is also important to note that the molar Gibbs free energy (Gibbs free energy per mole) for any state is equal to the chemical potential of that component (m).
Definition of Experimental Variables in Thermodynamics
The experimental variables provide practical (measurable) information about a specific material undergoing a process that can be used to solve thermodynamic problems involving said material. These values are well documented in the literature and are often found in the appendices of texts on the subject.
The coefficient of thermal expansion (a), is obtained from measuring the volume change of a material when the temperature of that material is changed at a constant pressure, and is given by:
![]()
Note: units are in reciprocal temperature (K)-1
The coefficient of compressibility (b), is determined by measuring the volume change of a substance as the pressure is increased while the temperature is held constant, and is given by:
![]()
Note: units are in reciprocal pressure (Pa)-1
The thermal behavior of materials is embodied in the concept of heat capacity (C), which is determined experimentally by precisely measuring the rise in temperature when a measured quantity of heat flows into the system. There are two different heat capacities. The first is for systems at constant and is noted as CP. The second is for systems at constant volume, noted as CV. The heat capacity at constant pressure can be obtained from the following relationship:
![]()
It is common to assume that the specific heat of a material is constant with respect to temperature in an effort to simplify calculations. In reality, the specific heat is a function of temperature and the previously mentioned assumption can result in significant error in modeling, depending on the material of study. The following relationship is used to determine the specific heat at constant pressure as a function of temperature:
![]()
Where a, b, and c are constants (available in said references covering thermodynamics) specific to a given material.
A similar relationship can be written for systems of constant volume:
![]()
Now is a good time to discuss an important difference between CP and CV. For systems at constant pressure, the absorption of heat results in both a temperature rise and an expansion in volume. For systems at constant volume, all of the heat acts to raise the temperature. This difference in definition means that more heat is required to raise the temperature of a substance one degree at constant pressure than at constant volume…CP>CV.
It can also be shown that for a monatomic gas that:
![]()
![]()
Where R is the ideal gas constant.
So, for an ideal gas:
![]()
![]()
At this point, we conclude that for any system where dW’=0 and a, b, and CP are known, the changes in all of the state function scan be computed.
Maxwell relations and energy functions in terms of temperature and pressure
Say that we can characterize a system with a series of inter-related state variables noted as X, Y, and Z. Since the variables are related, there must exist a relationship between them that, in the event we know two of the three variables, we can calculate the third. To explore this concept, let’s define a dependent variable, Z, as a function of two independent variables, X and Y, given by:
![]()
If the function is smooth, continuous with continuous derivatives (i.e. no discontinuities), an infinitesimal step in the process can be represented by:
![]()
The coefficients of this equation are certain explicit partial derivatives given by:
![]()
![]()
Utilizing the above equations and the defined experimental variables (a, b, Cp, Cv), we drive the following expressions:
![]()
![]()
![]()
![]()
![]()
![]()
The Maxwell relationship, which states in terms of our general equation:
![]()
can be used to show the relationships between the key terms of thermodynamics under changes in state functions. The following are such relationships:
![]()
![]()
![]()
![]()