PDF File: (Click to Down Load): Chapter2.pdf
Chapter 2 Polymer Physics
Concentrated Solutions and Melts
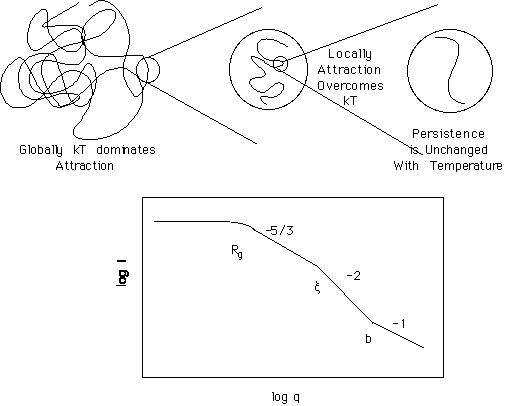
Chapter 1 discussed the statistical thermodynamics of an isolated polymer chain in a solvent. The conformation of an isolated polymer coil in solution is governed by maximization of entropy for the coil which, in the absence of interaction, leads to Gaussian scaling between the coil radius of gyration and the persistence length. The introduction of interactions can lead to two effects depending on whether the interactions are "short-range" or "long-range". Short range interactions lead to changes in the persistence length. Scaling is not effected by short range interactions except that the regime of scaling is broadened or diminished. Through increase or decrease in the persistence length, the coil can change sizes with goodness of solvent. This is reflected in the characteristic ratio, C = <R2q>/nl2, where <R2q> is the measured size of the coil in the theta state (Gaussian State). (For this calculation "n" is the number of bonds of length "l", so for a vinyl polymer "n" is twice the degree of polymerization and "l" is 1.54Å for a C-C bond.) The characteristic ratio is the conventional measure of short-range interactions, although, direct measurement of the persistence length is probably a more appropriate description of short-range effects such as bond rotation, bond angle, steric hindrances to bond rotation and steric hindrances due to solvent interaction. The measured size of a polymer coil in a non-theta solvent reduced by the theta state is historically described by the coil expansion factor, a2 = <R2>/<R2q>. The coil expansion factor includes long-range effects which lead to a discrete change in scaling due to the normal good solvent conditions. The coil expansion factor, changes continuously in figure 1.6 pp. 16 across the range of temperatures, although there is a discrete change in scaling at small shifts from the theta condition. Explanation of this inconsistency remained unsolved from the time Flory and Krigbaum predicted the good solvent scaling transition in 1972 and the development of the "Blob" concept by Edwards and de Gennes in the 1980's.
The picture of a single coil as it goes from the theta state to the expanded coil state involves an accommodation of changes in solvent conditions in two ways, 1) a discrete change in coil scaling and 2) a continuous variation in the size range over which this scaling is applicable. These two mechanisms lead, together, to the observed behavior of continuous coil expansion with temperature and the theoretical prediction of a discrete transition in scaling.
Some feeling for this problem can be given by a simple calculation in the absence of the "Blob" approach. Because the transition to expanded coil scaling is theoretically discrete, while the coil expansion is continuous, the implication in the absence of a "Blob" approach is that upon leaving the theta condition there is a predicted discrete change in the persistence length which accommodates the expanded condition. That is, at a position just slightly away from the theta-condition the coil will have a coil expansion factor, a, approximately equal to 1 despite the fact that any degree of good solvent will lead to a discrete transition in scaling to df = 1.67 from df = 2 for the theta condition. Equation 1.45 on pp. 12 states that the coil-size will scale with the number of persistence units by R* = b*n*3/5, in the expanded state. This can be set approximately equal to Rq = bqnq1/2, near the theta-temperature, leading to an approximate description of a predicted transition in structure at the theta to good-solvent transition region,
b* = bq nq1/2/ n*3/5
An added constraint on the system is that the primitive path for the coil remains unchanged, that is,
n*b* = nqbq
so,
n* = n
qbq/b*which yields,
b* = b
q/nq1/4, (Incorrect formula in the absence of the "Blob" concept)at the theta to expanded transition. For a degree of polymerization between 100 and 1000 b* is incorrectly projected to be 1/3 to 1/6 of b in the theta condition, immediately following the transition from Gaussian to expanded scaling. The projected change is discrete and strongly molecular weight dependent! The latter is completely contrary to the description of "b" as depending on short-range interactions. A discrete transition in "b" is not observed experimentally and, experimental measurements show a very low, and completely continuous thermal contraction of "b" that can be explained in terms of bond rotations as was done for a number of polymers in Flory's second book. The persistence length, "b", can be measured by a number of different experiments ranging from rheological measurements, dynamic light scattering, and static neutron or x-ray scattering measurements. The thermal dependence never shows this discrete transition.
Blobs:
A mass-fractal scaling regime is defined by a power law relationship between size of observation and mass as well as by two size limits. It was the latter issue of size limits to mass-fractal regimes which lead to a resolution of the thermal coil expansion issues discussed above as well as the current understanding of semi-dilute solutions.
The native state for polymer coil in dilute solution is the fully expanded coil (self-avoiding walk) with a mass-fractal dimension of 5/3. Consider such a coil, reflected in the high temperature end of figure 1.6 on pp. 16. The persistence length for this coil is "b" which has an extremely weak temperature dependence and can be considered fixed across the temperature range considered in figure 1.6. Between the coil diameter and the persistence length a single scaling regime is observed in an experiment such as scattering. As the temperature is dropped the diameter of the coil is reduced, while the persistence length remains unchanged and the dimension, at some size scales, remains 5/3. The coil thermally contracts because there is insufficient thermal energy to overcome a net long-range attraction between chain segments. This long-range attraction will eventually balance excluded volume to yield a Gaussian coil just before the coil collapses (left side of figure 1.6). It was the proposition of Edwards and de Gennes that the spatial range of this effective attraction between chain elements was not homogeneous, that is, this attraction first is observed on cooling at short spatial distances. Such an explanation is consistent with potentials such as the Leonard-Jones potential which decays with separation distance. The figure below shows a coil state intermediate between the fully expanded and the theta condition.

According to the "Blob" approach, the coil at an intermediate state of contraction between fully expanded and theta can be described as a polymer of nblob blobs which displays 5/3 dimension. Within the blob the thermal repulsion of segments have been overcome by the net attraction between segments leading to a Gaussian state with a coil dimension of 2. As the temperature is dropped the transition between Gaussian (at small sizes) and good solvent (at large sizes) shifts to larger and larger sizes (smaller q) until the entire coil is in the theta state at the theta temperature. The size of transition between good-solvent scaling and Gaussian scaling is called the correlation length or the "Blob" size. The persistence length remains unchanged while the overall coil size, as reflected in Rg, decreases as larger and larger range of size reaches the higher dimension (more compact).
If the Flory radius of the coil is written,
RF = aF n3/5
for the fully expanded coil and,
RFt = aF n1/2
for the theta coil, then the intermediate state can be written,
RF = x nx3/5 and x = aF (n/ nx)1/2 = aF z1/2
and,
RF = aF n1/2 nx1/10 = RFt nx1/10 = RFt (aF/x)1/5n1/10
This description of coil expansion is consistent with all theoretical predictions and is supported by some experiments although the transition in scaling which is expected is difficult to directly verify. The approach is termed the "Thermal Blob" approach. It will be seen that a similar approach can be used to describe concentration effects, termed the "Concentration Blob" approach.
Similarly, although of less general interest to polymer scientists is the theta to collapsed transition which occurs on lowering the temperature from the theta state in figure 1.6 pp. 16. This transition is of critical importance to proteins since the collapsed state represents the state of typical enzymes in biology which display tertiary structure. There is a wealth of recent literature on this subject, however, the coil to globule transition involves extremely complicated mathematical calculations which are far beyond the scope of this course. Generally, the transition involves local (short spatial distance) collapse of the Gaussian state to a more compact state which is governed by the local arrangement of mer units.
Concentration Effects:
Figure 2.1 shows a schematic model for what is expected as the concentration of a polymer solution is increased from the dilute condition which was discussed above to what has been termed the "Semi-Dilute" regime. As concentration is increased coils reach a point where, on average they just begin to overlap. This concentration is known as the "Overlap concentration". The overlap concentration, c*, can be calculated from,
c* Å N/Rg3 = N1-3n = N-4/5
On pp. 37 Doi discusses the scaling features of a polymer coil in the semi-dilute regime. For concentrations above c* the polymer coil can be considered to be composed of c/c* chains in a volume which is occupied by one dilute chain. For a dilute chain in a good solvent the chain experiences repulsive interactions between chain elements which lead to excluded volume and good solvent scaling. As the concentration is increased beyond the overlap concentration the repulsive interactions that lead to good solvent scaling are screened by the presence of other chains within the coil.
The concept of screening can be seen in many physical systems and the idea was developed in electrostatics to describe concentrated charge systems, Debye-Huckel screening length. A simple system where the effect of screening can be observed is one where it is desired to determine the direction "west" in a forest at sunset. For a thin forest the sun shines through the trees so the direction of "west" can be easily determined. As the forest becomes denser the trees begin to shield the sun and the observer can only see a faint glow at sunset with no associated direction. The faint glow is a "mean field" which lacks direction. The net effect of this mean field in terms of determining the direction "west" is zero.
If one considers that the forest has a sharp edge then there is some distance from the edge of the forest where the direction "west" can still just be determined. This distance gets smaller and smaller as the density (concentration) gets higher and higher. For the forest this distance to the edge is the screening length,
x. At high forest density the screening length approaches the size of a tree. At low forest density it approaches the size of the forest.For a polymer solution, screening "turns off" the repulsive interaction which leads to excluded volume and good solvent scaling. When excluded volume is turned off the coil takes on Gaussian scaling. This occurs at large spatial distances where the potential becomes a mean field, just as at long distances from the edge of the forest the sunset becomes a faint, uniform glow. At small spatial distances the coil retains good-solvent scaling in the semi-dilute regime. The concentrated regime is concentrations above that where the screening length equals the statistical segment length.
The scaling behavior in terms of the "concentration blob" is inverse to that of the "thermal blob", that is at large spatial distances (small q) the coil is Gaussian, and at small spatial distances (high q) the coil displays good solvent scaling. The situation can be considered, also, from the other the concentration spectrum. That is, a solid polymer melt is entirely Gaussian. As this polymer melt is swollen in a good solvent it is first, short spatial distances which display good solvent scaling. As more solvent is added, the range of sizes where good solvent scaling is observed increases until a dilute condition is reached.
As with the thermal blob, the concentration blob can be used to calculate the size of a polymer coil,
RF =
x nx1/2This reflects a Gaussian distribution of blobs of size x. x should be a function of concentration. Also, at the overlap concentration x is approximately equal to RF0 so,
x
= RF0 f(c/c*), where,RF0 Å aF N3/5
Since the concentration blob involves subunits of the coil which are governed in size by the thermodynamics of interaction, it should be clear that
x can not have a molecular weight dependence. c* = N/ RF03 = N-4/5, so c/c* is proportional to N4/5 and to remove the molecular weight dependence,x
= RF0 (c/c*)-3/4The latter expression has been verified experimentally.
Within a concentration blob good solvent scaling is followed so
x = aF (N/nx)3/5, so nx is equal to (c/c*)5/4, and,RF =
x nx1/2 = RF0 (c/c*)-3/4 (c/c*)5/8 = RF0 (c/c*)-1/8The latter being equation 2.84 of Doi, pp. 38.
Flory Huggins Theory: Section 2.1.1
Flory-Huggins theory has already been derived in Intro to Polymers. The Flory-Huggins Equation describes the Helmholtz mixing free energy per lattice site, kTfm(f) for a Polymer/Solvent system in terms of the volume fraction polymer, f, the degree of polymerization, N, and the Flory-Huggins interaction parameter, c = (z/2kT) [epp + ess - 2eps], where z is the coordination number for the lattice,
fm(f) = f lnf / N + (1-f) ln(1- f) + c f (1- f)
The features of this equation should be familiar to you. The Helmholtz (Volumetric) free energy change on mixing for a given system is given by the above expression times the number of lattice sites in the system, W, Fm(W,f) = W kT fm(f).
Chemical Potential and Osmotic Pressure:
The chemical potential, here mp or ms, for one component of a mixture is the derivative of the Gibbs free energy for the system with respect to the number of moles of that component. The Gibbs free energy is related to the Helmholtz free energy by, G = F +PV. For the Flory lattice system the volume equals the number of lattice sites time the volume of one site, V = WVc, where W = ns + nPN and N is the degree of polymerization. Changing the number of moles of one component in the Flory lattice model, while retaining the number of moles of the other component will result in a change in the lattice size, W and the volume fraction f, and system volume, V. This means,
m
s: np, T, P constant (f, P, T) - m0s(T) = (dF/dW)f,T(dW/dns)np +(dF/df) W,T (df/dns) np + PVc=
Where
m0s(T) is the chemical potential of the pure solvent.From the definition of W, (dW/dns)np = 1; and given that f = npN/(np N + ns) = npN/W, so (df/dW)np = -npN/W2. (df/dns)np = (df/dW)np (dW/dns)np = -npN/W2 = -f/W. (dF/dW)f,T = kT fm (f), and (dF/df) W,T = W kT (dfm/df) W,T , so,
m
s: np, T, P constant (f, P, T) = m0s(T) + kT (fm (f) - f (dfm/df) W,T )+ PVcand through a similar approach,
m
p: ns, T, P constant (f, P, T) = m0p(T) + kT (fm (f) - (1-f) (dfm/df) W,T )+ PVc
Osmotic Pressure:
The osmotic pressure is the excess pressure needed to make a solution with a polymer have the same chemical potential as a pure solvent phase at the same temperature,
m
s: (f, P+P, T) = ms(f=0, P, T)At
f = 0 fm = 0 so ms(f=0, P, T) = m0s(T) + PVc, and using the above expression,m
s(f, P+P, T) = m0s(T) + kT (fm (f) - f (dfm/df) W,T )+ (P+P)Vc,so,
PVc = kT (fm (
f) - f (dfm/df) W,T )+ PVc + P Vcand
P
= (kT/Vc) (f (dfm/df) W,T - fm (f))fm(
f) = f lnf / N + (1-f) ln(1- f) + c f (1- f)(
dfm/df) W,T = lnf/N + 1/N - (1+f)/(1-f) - ln (1-f) + c(1 - 2f)so,
f
(dfm/df) W,T - fm (f) = f/N - ln(1- f) - f (1-f)/(1-f) + c {f(1 - 2f)- f (1- f)}= f
/N - ln(1- f) - f - c f2for f<1, ln(1-f) = -{f + f2/2 + f3/3 + f4/4 +...} and,
P
= (kT/Vc) [f/N + (1/2 - c) f2 + f3/3 + f4/4 +... ]This is a viral expansion with (1/2 - c) being the second viral coefficient. For small concentrations, f << 1,
P
= (kT/(NVc))f = np kT/Vc (van't Hoff's law)This is valid when
f << 1/{N(1/2 - c)}, so for very low concentrations for high molecular weight, N. For large N the first term drops out and P Å (kT/Vc) (1/2 - c) f2, which is independent of molecular weight and follows a power 2 in volume fraction polymer. The schematic below shows the expected behavior of log (P/C) in log C, (see Doi figure 2.2 pp. 25),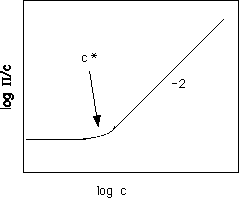
At the
q condition c = 1/2, and the second viral coefficient goes to 0. The derivation of the value of c at the theta point will be discussed next.Osmotic Pressure For Expanded Coils.html
Phase Separation:
The Flory-Huggins equation, with
c=0, yields a free energy curve as shown below with a single minimum.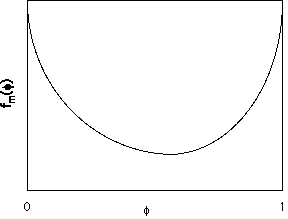
For a polymer of N = 100 and
c from 0 to 2 in 0.5 increments the Flory-Huggins equation yields: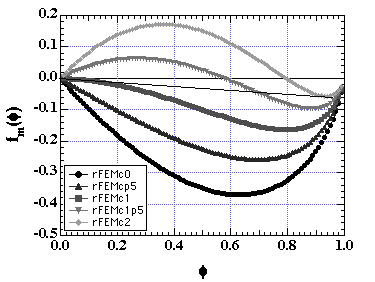
Which means that phases will separate into an almost pure solvent phase and a mixed phase that is mostly polymer (see Doi pp. 27). The critical point occurs between
c = 0.5 and c = 1.0, where the curvature of the free energy of mixing begins to curve upwards. Increasing c corresponds with lowering of the temperature since c = k/T. The critical point can be found from the value of f where the first and second derivatives of fm with f go to 0.The first derivative was calculated above,
(
dfm/df) = lnf/N + 1/N - (1+f)/(1-f) - ln (1-f) + c(1 - 2f)and,
(
d2fm/df2) = 1/( f N) - 1/(1-f) - 2 c = 0(
d3fm/df3) = -1/( f2 N) + 1/(1-f)2 = 0The latter yields
fc = 1/(1 + ÃN), and using this value in the second derivative yields:so, cc Å 1/2 (1 + 1/ÃN)
Concentration Fluctuations in Polymer Solutions:
(Follows Gert Strobl "The Physics of Polymers 2'nd Ed. 1997 Appendix A4 but follows Doi section 2.2 fairly closely)
A polymer in dilute solution is a single phase but contains concentration fluctuations related to chain connectivity and random thermal motion. The Flory-Huggins approach ignores these concentration fluctuations so is not applicable near the critical point where fluctuations are high and is really not appropriate for discussions of small-scale features except in an average sense. The Flory-Huggins statistical model uses an average interaction energy which is termed a "mean field" approach. As concentration is increased in a polymer solution, screening leads to a reduction in the effect of connectivity based monomer density fluctuations. In a pure melt all connectivity based segmental fluctuations, of this kind, are screened leading to Gaussian scaling.
Much of modern polymer theory is based on an understanding and description of concentration fluctuations. This is because a description of such fluctuations are a natural way to describe random systems with statistical features. Fluctuations in density can be described in terms of a series of wavelengths, that is, any distribution of density in space can be decomposed into a series of sin waves of different magnitude. For each wavelength there is an associated wave number, k = 2p/l, associated with that type of fluctuation. The amplitude of a density fluctuation at wave number k (and wavelength l) which contributes to the density profile of a sample in space, r, can be denoted fk.
1) Fluctuations of wavenumber "k" can be considered independently of other wavenumber fluctuations.
2) Incompressibility is an assumption of almost all theoretical approaches so fk refers to one component of a mixture but the other component is just - fk, so fluctuations of component A are matched by opposing fluctuations of B in the opposite direction to yield an average concentration for each wavenumber.
Density fluctuations of fk follow Boltzman statistics so the probability of a fluctuation of size fk is given by,
p(fk) Å exp(-ak fk2/2kT)
where ak is the inverse of the response of the density, fk, to a potential field, Yk,
f
k = Yk/ak = ak Yk(The increase in free energy, dG associated with a concentration fluctuation, fk, is given by,
d
G = ak fk2/2 = Yk dfk)The mean square value, < fk2> = kT/ ak = kT ak
The scattering function per lattice site of volume Vc, Sc(q=k) is related to this mean square fluctuation by,
Sc(q) = kT ak/Vc
The calculation of a scattering function, Sc(q=k), is the equivalent of calculation of response functions, ak.
Random Phase Approximation (RPA):
One of the major accomplishments of the density fluctuation approach described above was the calculation of the scattering function for a polymer/polymer mixture and for block copolymers in the single phase state. These scattering functions are composed of Debye scattering functions which describe the coils in a dilute solution at the theta temperature. Prior to the development of the random phase approximation (early 1980's) it was not possible to directly determine the interaction parameter for polymer blends from scattering data. This is now the primary method of determination of the interaction parameter. Additionally, application of the RPA approach to block copolymers is the primary method of determination of the thermodynamics of these systems. If one were to combine all polymer physics papers from the last 5 years more than half would involve in some way use of the RPA approach. Despite the fact that this approach is exclusively used with scattering analysis, it is of pivotal importance to have some understanding of it in order to understand recent literature as a whole.
The RPA approach is an extension of the composition fluctuation ideas presented above. Consider an athermal mixture of two polymer chains, A and B. Consider that the B chains have 0 contrast so are not observable. If a potential, Yk, is applied to this system that only acts on "A" chains and which leads to excitation of a concentration fluctuation of wave vector "k", fk, we can write,
f
k = ak0 Ykwhere ak0 is the collective response coefficient for lattice units of chain "A" under athermal conditions (hence the superscript 0) in a mixture with chains "B". Under the discussion above, ak0, is associated with the scattering from the mixture of "A" and "B" chains.
A fluctuation of concentration in "A" leads to a negative fluctuation of "B" due to incompressibility.
f
k = fkA = -fkBThis response of "B" units to a fluctuation in "A" units reflects the internal induction of the system. "B" units respond as if they were subjected to a potential Yk even though "B" units do not respond to the external field which is applied. Yk is called the "internal field".
A-chains respond to both the internal field, Yk, as well as to the external field Yk.
f
k = akAA (Yk + Yk)where akAA is the single-chain response coefficient of "A" units response to forces acting on other "A" units. This is different than ak0 which reflects the response of an "A" unit to an external field. For chains in a melt it is assumed that the Gaussian state is displayed due to screening so analytic forms based on the Debye scattering function apply to describe the single-chain response coefficients. That is, we already have an analytic form which describes scattering associated with akAA.
"B" units respond only to the internal field, Yk, since the external field, Yk, acts only on "A" units as introduced. Thus,
f
kB = -fk = akBB (Yk)The collective response coefficient, ak0, is associated with the scattering from the mixture of "A" and "B" chains. In order to determine ak0 from the known Debye functions for akAA and akBB, the induced field, Yk, must be expressed as a function of the known functions and the applied field, Yk,
Y
k = Yk akAA/( akAA + akBB)Through addition of the two expressions above. This expression can then be used in the expression for fk above to yield,
f
k = Yk { akBB akAA/( akAA + akBB)}and by comparison with the first expression of this section yields,
1/ ak0 = 1/ akAA + 1/ akBB
The latter implies that the inverse of the scattering function for a polymer blend is an inverse sum of the scattering functions for the two components.
For non-athermal systems, an external potential Yk leads to a concentration wave fk which produces a molecular field, c' fk, where c' = 2ckT/Vc. If c' is positive the field is enhanced and if c' is negative the external field is diminished.
f
k = ak0 (Yk + c' fk)This can be solved for fk to yield,
f
k = ak0 Yk/(1 - c' ak0)The non-athermal collective response coefficient, ak, is associated with the scattering from a non-athermal polymer blend. This response coefficient can be directly obtained from the above expression by comparison with the definition of the collective response coefficient,
a
k = fk/ Yk = ak0/(1 - c' ak0)or
1/ ak = 1/ ak0 - c'
Using the previous expression for 1/ ak0 we have,
1/ ak = 1/ akAA + 1/ akBB - 2ckT/Vc
(For a polymer solution akBB is a constant in k.)
Block Copolymers and the Random Phase Approximation:
For an athermal system composed of a block copolymer of A and B segments, the description of concentration fluctuations parallels that for a polymer blends except that response coefficients related to the connectivity of A and B chains must be included. akAB reflects the reaction of A units to a force acting on B units in the same chain (at wave vector k). A response coefficient akBA reflects the reaction of B units to a force acting on A chains (at wave vector k). In parallel with the athermal blend derivation above,
f
k = akAA (Yk + Yk) + akAB Ykand
f
kB = -fk = akBB (Yk) + akBA (Yk + Yk)The last term representing a force acting on an A unit and the response of a B unit so includes the internal and external fields. The internal field, Yk, can be removed by summation of the two equations under the assumption of incompressibility, fkB = -fk,
Y
k(akAA+ akAB + akBB + akBA) = -Yk (akBA + akAA)Y
k = -Yk (akAA + akBA)/(akAA+ akAB + akBB + akBA)This can be substituted in the expression for fk yielding,
f
k = Yk {akAA - [akAA + akAB] (akAA + akBA)/(akAA+ akAB + akBB + akBA)}and,
a
k0 = fk/Yk={akAA - [akAA + akAB] [akAA + akBA]/(akAA+ akAB + akBB + akBA)}= (akAA akAA + akAA akAB + akAA akBB + akAA akBA - akAA akAA - akAAakBA - akABakAA- akABakBA)
(akAA+ akAB + akBB + akBA)
ak0 = (akAA akBB - akABakBA)/(akAA+ akAB + akBB + akBA)
The latter representing the RPA for athermal block copolymers. The thermal system can be calculated using the same approach as for thermal blends given above,
1/ ak = 1/ ak0 - c' = (akAA+ akAB + akBB + akBA)/(akAA akBB - akABakBA) - 2kTc/Vc
To obtain the scattering functions we substitute,
a
k=qAA = Vc fNASD(RAq)/kTand
a
k=qBB = Vc (1 - f) NBSD(RBq) /kTwhere Ni is the degree of polymerization for chains of type "i",
f, is the dilution of chains A in the block copolymer, SD is the Debye scattering function for a polymer coil and Ri is the coil's Gaussian radius of gyration. The Debye function is the Fourier-transform of the pair distribution function g(r) for the pairs of type AA or BB.To calculate
akAB we need the pair distribution functions for the probability of finding a B or A monomer at a distance r from each other. The latter can be analytically solved as a function of the single chain structures. One result of this is that akAB = akBA. The functional form is,a
k=qAB = Vc (NABSD(R0q) - fNASD(RAq) - (1 - f) NBSD(RBq))/(2kT)where NAB = NA + NB, and R02 = RA2 + RB2.
Block copolymers display a "natural" correlation distance which is a result of segregation of A and B blocks in a single phase melt. This "natural" distance of segregation is reflected in the athermal equation for instance.
a
k0 = (akAA akBB - akABakBA)/(akAA+ akAB + akBB + akBA)Consider the summation of response coefficients as a summation of Debye functions. For a 50/50 block copolymer NA = NB, and RA Å RB, then R0 is Ã2RA, i.e. R0 is bigger than RA. It can be easily verified that the subtraction of two Debye functions of differing R yields a curve with a correlation peak (see figure below). Thus, even in the single phase melt, block copolymers display a correlation peak.
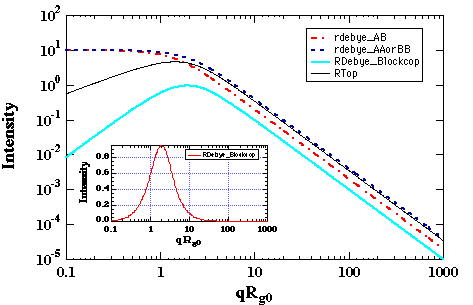
Variation of c' in the thermal system leads to the determination of a critical point where the intensity becomes infinite as shown below:
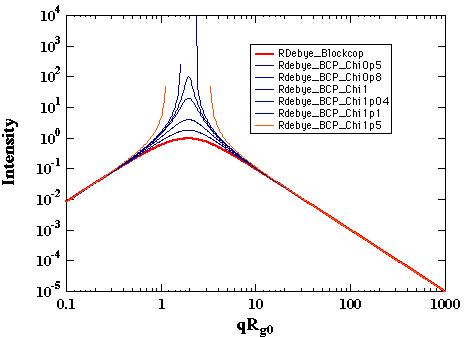
For symmetric diblock copolymers ccNAB = 10.4. This is the lowest value for ccritical, i.e. other compositions will have higher values. This value should be compared with the critical c for the same two polymers in a symmetric binary blend, ccN = 2. The higher value for the critical point in a block copolymer reflects the connectivity of the polymer chains which suppresses phase separation to a higher value of c (lower temperature).
When phase separation occurs in a block copolymer the domain size is restricted by the connection of the A and B chains. This leads to a variety of micro-phase separated structures. When one chain is much shorter than the other, NA<<NB, spherical domains form. For more closely matched molecular weights rods of the minor phase form. When NA Å NB, the system forms lamellar domains. The size of these domains is governed by thermodynamics as discussed below.
Domain Size in Phase Separated Block Copolymers:
The size and separation distance of lamellar domains (for example) can be predicted using thermodynamics. The change in Gibbs free energy, DG, for the transition from a homogeneous system to the micro-phase separated system is composed of an enthalpic term, DH, which has contributions from bulk, DHbulk, and interface, DHint, a change in entropy associated with A-B junction points becoming located at the interface, DSint, and a change in entropy associated with stretching the chains, DSstr. The bulk enthalpy change is given by Flory Huggins theory as,
D
Hbulk = - kTcNABfA(1-fA)The interfacial enthalpy is associated with an interfacial area, A, a transition layer thickness dt,
D
Hint = + kT c A dt/VcThe loss in entropy by location of A-B junctions at the interface is given by,
D
Sint = k ln(dt/(dA + dB)) = k ln(dt/dAB)where dA is the thickness of the A layer and dB is the thickness of the B layer and dAB is the repeat period for the lamellae. The loss in entropy due to stretching of the chains is given by,
D
Sstr = -kb2(dAB/R0)2Also, the volume of a chain is given by Vc NAB = A dAB
D
G = DHbulk + DHint - T DSint - T DSstrbecomes,
D
G/kT = - cNABfA(1-fA) + c A dt/Vc + ln(dt/dAB) + b2(dAB/R0)2Setting the derivative with respect to "A" to 0, neglecting the "ln" term which does not have a significant derivative (using dAB = Vc NAB / A in the last term),
(1/kT) dDG/dA = c dt/Vc - 2b2(Vc NAB /R0)2/A3 = 0
yields,
A Å Vc (2 NAB2 /( c dt R02))1/3
using R02 = Vc2/3 NAB
A3 Å Vc7/3 NAB/(c dt)
and
dAB = NAB2/3 Vc2/9 (c dt)1/3
This molecular weight dependence has been observed experimentally.