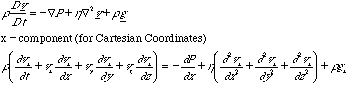
Reynold's Equation:
PDF File: (Click to Down Load): Reynold's Equation.pdf
=> Back to Chapter 2
=> Back to TOC
=> To Syllabus
Obtain the x-velocity distribution as a function of y for simple shear flow between parallel plates.
Consider a fluid between two parallel plates. The top plate moves at a velocity V0 and there is a pressure drop in the x-direction, parallel to the plates. There is no velocity or pressure drop in the z-, or y-directions, y is normal to the plates. The effects of gravity are ignored and the flow is steady-state. Assume Newtonian behavior.
Under these conditions, only the x-component of the Navier-Stokes equation is needed.
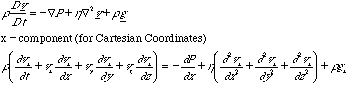
Steady state means that the first term (derivative in time) is 0. There is no y or z velocity so the last two terms are 0. There is not change in the x-velocity with x so the second term is 0. On the right side there is a pressure drop in x and the x-component of velocity only changes in the y-direction . The gravity term is dropped as it is assumed that there is no gravity effect.
For Newtonian flow hd2vx/dy2 = dtyx/dy. The Navier-Stokes rate of change of momentum balance becomes:
![]()
Of primary interest is the velocity distribution vx(y) that can be obtained by integration of this equation between definite limits. vx at y = 0 is 0 and vx at y = H, where H is the gap distance, is V0. Double integration yields:
![]()
vx(y=0) = 0, so C2 = 0. vx(y=H) = V0, so C1 = hV0/(H dP/dx) - H/2, then,
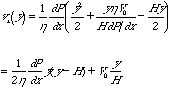
The first term is quadratic with a maximum at H/2 as might be expected for a pressure driven flow. The second term is linear, reflecting a constant rate of strain for simple shear in the absence of a pressure driving force. The two components are summed. This equation is a simple form of the Reynolds equation.
The Reynold's equation for velocity is integrated in y to yield the integrated flow rate, qx,
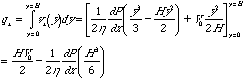
The Reynold's number for this system is given by, Re = HrV0/h, where r is the density. The integrated flow rate can be rewritten,
![]()
The mass flow rate depends on the Reynold's number.